How do you find the max or minimum of #f(x)=4x-x^2+1#?
2 Answers
Explanation:
#f(x)=-x^2+4x+1larrcolor(blue)"in standard form"#
#"with "a=-1,b=4" and "c=1#
#• " if "a>0" then f(x) has a minimum "uuu#
#• " if "a<0" then f(x) has a maximum "nnn#
#"here "a=-1<0rArr"f(x) has a maximum"#
#"the max/min is at the vertex of the parabola"#
#"to find the vertex use "color(blue)"completing the square"#
#rArrf(x)=-(x^2-4x-1)#
#color(white)(xxxxxx)=-(x^2+(-2)x+4-4-1)#
#color(white)(xxxxxx)=-(x-2)^2+5#
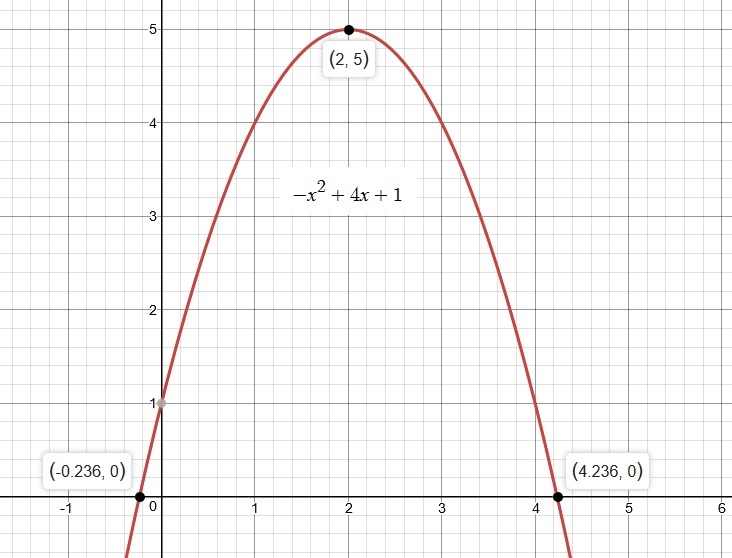
#rArr"vertex at "(2,5)#
#rArr"maximum at "(2,5)#
graph{(y+x^2-4x-1)((x-2)^2+(y-5)^2-0.04)=0 [-10, 10, -5, 5]}
Maximum is at :
Explanation:
Given:
The Standard Form of a Quadratic Equation is:
If
the y coordinate value of the vertex represents a Minimum
If
the y coordinate value of the vertex represents a Maximum
Hence, we have a Maximum for our problem.
Also, remember that
Vertex:
From .... (1) we observe that
x coordinate of the vertex:
Substitute the value of the x coordinate in (1) to get the y coordinate value
Hence,
Maximum is at :
Analyze the graph below to understand the behavior of the quadratic:
Hope you find this solution useful.

