How do you find the max or minimum of #f(x)=x^2-8x+2#?
2 Answers
Check the coefficient of
Explanation:
A quadratic equation in standard form is
To calculate the
We know that
So, we have
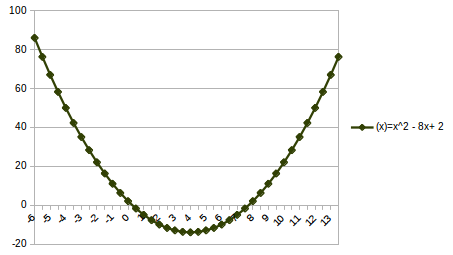
graph{(x^2 - 8x + 2 - y)(-14 -y)=0 [-11.82, 20.22, -15.38, 0.64]}
The first derivative zero is the extrema. The second derivative sign indicates the direction, or use the sign of the first derivative on each side.
Explanation:
Negative at
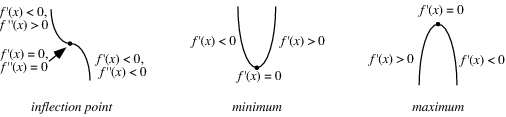
First Derivative Test
Suppose f(x) is continuous at a stationary point x_0.
-
If
#f^'(x)>0# on an open interval extending left from x_0 and#f^'(x)<0# on an open interval extending right from x_0, then f(x) has a local maximum (possibly a global maximum) at x_0. -
If
#f^'(x)<0# on an open interval extending left from x_0 and#f^'(x)>0# on an open interval extending right from x_0, then f(x) has a local minimum (possibly a global minimum) at x_0. -
#If f^'(x)# has the same sign on an open interval extending left from x_0 and on an open interval extending right from x_0, then f(x) has an inflection point at x_0.
Weisstein, Eric W. "First Derivative Test." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/FirstDerivativeTest.html
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.
Referenced on Wolfram|Alpha: First Derivative Test
Second Derivative Test
Suppose f(x) is a function of x that is twice differentiable at a stationary point x_0.
-
If f^('')(x_0)>0, then f has a local minimum at x_0.
-
If f^('')(x_0)<0, then f has a local maximum at x_0.
The extremum test gives slightly more general conditions under which a function with f^('')(x_0)=0 is a maximum or minimum.
If f(x,y) is a two-dimensional function that has a local extremum at a point (x_0,y_0) and has continuous partial derivatives at this point, then f_x(x_0,y_0)=0 and f_y(x_0,y_0)=0. The second partial derivatives test classifies the point as a local maximum or local minimum.
Define the second derivative test discriminant as
D = f_(xx)f_(yy)-f_(xy)f_(yx)
= f_(xx)f_(yy)-f_(xy)^2.
Then
-
If D>0 and f_(xx)(x_0,y_0)>0, the point is a local minimum.
-
If D>0 and f_(xx)(x_0,y_0)<0, the point is a local maximum.
-
If D<0, the point is a saddle point.
-
If D=0, higher order tests must be used.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.


