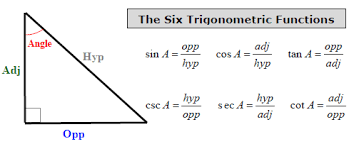
How do you find the measure of each of the angles of a triangle given the measurements of the sides are 7, 24, 25?
1 Answer
Apr 9, 2018
Explanation:
Pythagoras' theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle.
It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides
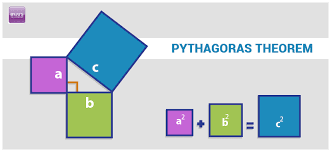
Given
Hence it's a right triangle with