How do you find the parametric equations of a circle?
1 Answer
We'll start with the parametric equations for a circle:
#y = rsin t#
#x = rcos t#
where
If you know that the implicit equation for a circle in Cartesian coordinates is
We will take the equation for
#x/r = cos t#
#t = arccos (x/r)#
Now substitute into the equation for
#y = rsin arccos(x/r)#
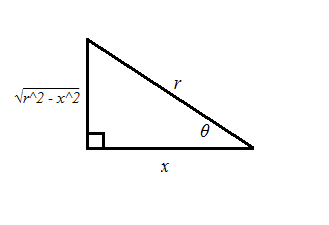
Thus,
#y = r*sqrt(r^2 - x^2)/r#
This simplifies to
#y = sqrt(r^2 - x^2)#
If we square this entire deal and solve for
#r^2 = x^2 + y^2#
which is precisely the equation for a circle in Cartesian coordinates.

