How do you find the parametric equations of a curve?
1 Answer
It depends on the curve you're analyzing,
In general, finding the parametric equations that describe a curve is not trivial. For the cases that the curve is a familiar shape (such as piecewise linear curve or a conic section) it's not that complicated to find such equations, due to our knowledge of their geometry.
As an example of a curve that's difficult to find the parametrization, just close your eyes and draw any curve on a piece of paper. Chances are that curve has a complicated description, and even if you found the equations describing it, it would probably be hard to work with them.
For problems that have these kind of difficulties, it's interesting to use numerical methods (such as piecewise linear approximations).
An example that's not comprised of combinations of line segments or conic sections:
The cycloid is a curve with many interesting properties. Finding the parametric equations that describe it is very useful.
A cycloid is the curve generated by rotating a circle (of, say, radius
The parameter adopted will be the angle described by the point intially at the origin, the center of the circle and the point of contact between the circle and the
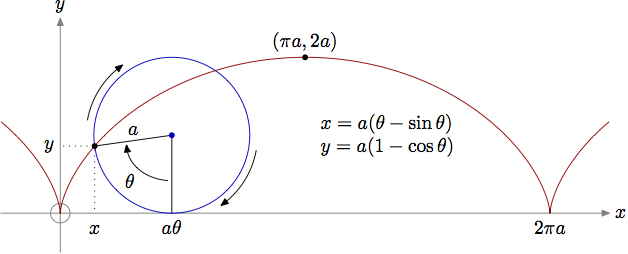
Basic geometry* will give us the equations:
*The

