How do you find the perimeter of an equilateral with an altitude of #6sqrt3# cm?

Question

1610 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-11-30T21:38:02

Apply the Pythagorean theorem to solve for the side length and find that the perimeter is #36"cm"#

Drawing it out, we obtain the following picture:
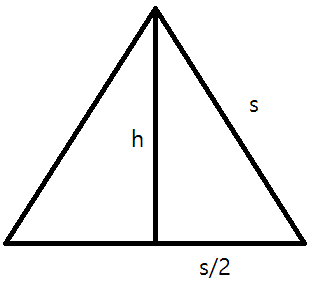
enter image source here

Our goal is to find the perimeter, that is, #s+s+s=3s#

Looking at the right triangle with the sides marked in the picture, we can apply the Pythagorean theorem to get

#(s/2)^2 + h^2 = s^2#

#=> s^2/4 + h^2 = s^2#

#=> h^2 = 3/4s^2#

#=> s^2 = (4h^2)/3#

#=> s = sqrt((4h^2)/3)#

Substituting in our value for #h#, we obtain

#s = sqrt((4*(6sqrt(3))^2)/3)#

#=sqrt((4*108)/3)#

#=sqrt(144)#

#=12#

Thus #3s = 3*12 = 36#

So the perimeter is #36"cm"#