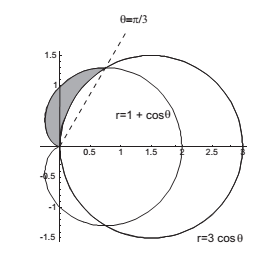
How do you find the region inside cardioid #r=1+cos(theta)# and outside the circle #r=3cos(theta)#?

Question

109963 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-09-17T15:22:49

It is #pi/4#

Find the intersection points of the curves hence we have that

#3cosθ=1+cosθ=>cosθ=1/2=>θ=+-pi/3#

The saded area is

(cardiod area from pi/3 to pi)-(cricle area from pi/3 to pi/2)

The cardiod area is

#int_(pi/3)^(pi) 1/2*(1+cosθ)^2dθ=pi/2-9/6*sqrt3#

and the circle area is

#int_(pi/3)^(pi/2) 1/2*(3*cosθ)^2dθ=(3pi/8)-9/16*sqrt3#

Hence the shaded area is #pi/8#

The total amount is #2pi/8=pi/4#

A graph for the curves is

enter image source here