How do you find the slope and intercept of #y = 4/3x - 3#?
2 Answers
Explanation:
This equation is in slope-intercept form:
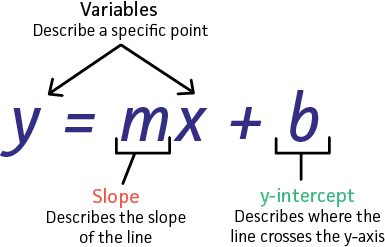
We know the slope is the value multiplied by
To find the
Add
Multiply both sides by
Therefore, the
To find the
Therefore, the
Hope this helps!
Slope
Explanation:
This equation is in slope-intercept form
We can find the
Therefore, our slope is
Hope this helps!


