How do you find the slope and y intercept of #y + 1 = 1(x + 2)#?

Question

5792 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-08-02T01:05:35

The slope is 1.

The y-intercept is at (0, 1).

#y + 1 = 1(x+2)#

This equation is in point-slope form:
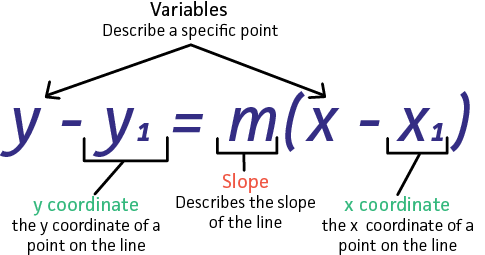
enter image source here

Based on the picture, we know that the slope is the value multiplying #x-x_1#, so the slope is #1#.

To find the #y#-intercept, plug in #0# for #x# and solve for #y#:
#y + 1 = 1(x+2)#

#y + 1 = 1(0+2)#

#y + 1 = 2#

#y = 1#

Therefore, the #y#-intercept is at #(0, 1)#.

Hope this helps!

Answer 2 · 2018-08-02T01:24:04

Slope #1#, #y#-intercept of #1#

It may be more intuitive by converting this equation into slope-intercept form

#y=mx+b#, with slope #m# and a #y#-intercept of #b#. Let's start by distributing the #1# on the right to get

#y+1=x+2#

Next, let's subtract #1# from both sides to get

#y=x+1#

We see that our slope is #1#, and so is our #y#-intercept.

Hope this helps!