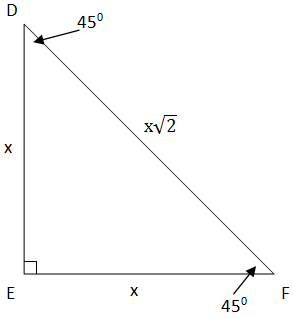How do you find the third side of a right triangle if the base is x = 20m, and height is y = 20m?
1 Answer
Jun 6, 2015
The third side is the hypotenuse, which is
This is an example of an iscoseles right triangle, in which the angles are 45-45-90 degrees. In an iscoseles right triangle, the base and height are the same. The hypotenuse is the missing side and is equal to
We can use the Pythagorean theorem to prove this: