What is the Pythagorean Theorem?
2 Answers
The Pythagorean Theorem is a relation in a right-angled triangle. The rule states that 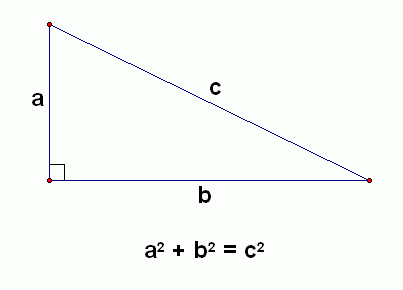
Trust me, it's a very helpful topic in Geometry and you can learn more about it down below!
Explanation:
The Pythagorean Thereom (found by Pythagoras aka Pythagoras of Samos) is used to find the length of a side of a right triangle using the formula
A right triangle has two "legs" and a hypotenuse. A hypotenuse is the longest side of a right triangle and is always the opposite of the right angle corner. The legs can be a or b (it doesn't matter which is
 )
)
In this case, lets say that
After substituting...
After simplifying...
Now, solve it!
Whoa, whoa, wait a second before you finalize that as the answer! We can simplify this. It's just not
Remember, we don't use the Pythagorean Theorem just for the hypotenuse! We can use it for the other sides, too! Ex:  )
)
In this problem, we know the hypotenuse, but we need to find out what one of the "legs" is. Lets say that
After substituting...
After simplifying...
Leave
There! We have it! I hope you have a better clarity of the Pythagorean Thereom and understand it! My source (despite the images) is my mind! Sorry if my answer is too long!


