Question

What is the length of the ladder if a ladder of length L is carried horizontally around a corner from a hall 3 feet wide into a hall 4 feet wide?

Answer 1

Consider a line segment running from `(x,0)` to `(0,y)` through the interior corner at `(4,3)`.
The minimum length of this line segment will be the maximum length of ladder that can be maneuvered around this corner.

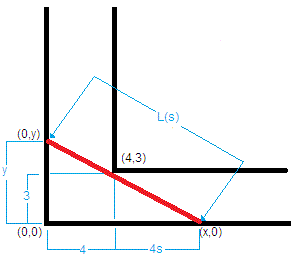
Suppose that `x` is beyond `(4,0)` by some scaling factor, `s`, of 4, so
`x = 4 + 4s = 4 (1 + s)`
[watch for the `(1+s)` showing up later as a value to be factored out of something.]

By similar triangles we can see that
`y = 3 (1 + 1/s)`

By the Pythagorean Theorem, we can express the square of the length of the line segment as a function of `s`
`L^2(s) = 3^2 (s^(-2) + 2s^(-1) + 1) + 4^2 (1 + 2s + s^2)`

Normally we would take the derivative of L(s) to find the minimum but in this case it is easier to take the derivative of `L^2(s)`.
(Note that if `L(s)` is a minimum as `s=s_0`, then `L^2(s)` will also be a minimum at `s=s_0`.)

Taking the first derivative of `L^2(s)` and setting it to zero, we get:
`3^2 ( -2s^(-3) - 2s^(-2) ) + 4^2 ( 2 - 2s) = 0`

Multiplying by `s^3` and then factoring out `2 (1+s)`
allows us to solve for `s`

`s = (3/4)^(2/3)`

Plugging this value back into the equation for `L^2(s)` and taking the square root (I used a spreadsheet), we get
the maximum ladder length `= 9.87 feet` (approx.)