If theta = cot^(-1)(-1/sqrt(3))
the
the ratio ("opposite side")/("adjacent side") of the defining triangle
must be
color(white)("XXXX")(-1):(sqrt(3)) (or equivalently (1):(-sqrt(3)))
We therefore have the conditions below: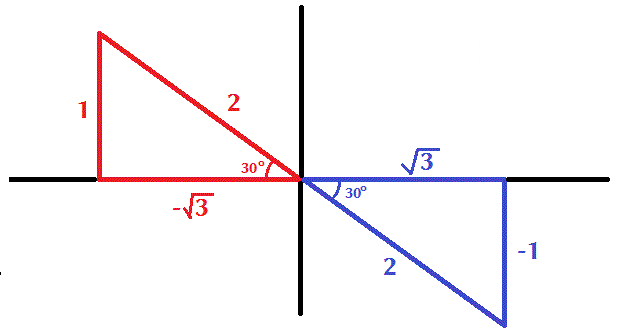
These are standard reference triangles and based on their quadrants the corresponding angles (within the range [0,360^o]
are
color(white)("XXXX")180^o - 30^0 = 150^o = (5pi)/6 radians
and
color(white)("XXXX")360^o - 30^o = 330^o = (11pi)/6 radians
These can be combined and include angles outside the [0,2pi] range as
color(white)("XXXX")theta = 150^o +n*180^o
or
color(white)("XXXX")theta = (5pi)/6 + n*pi
color(white)("XXXX")color(white)("XXXX")color(white)("XXXX")for AA n in ZZ

