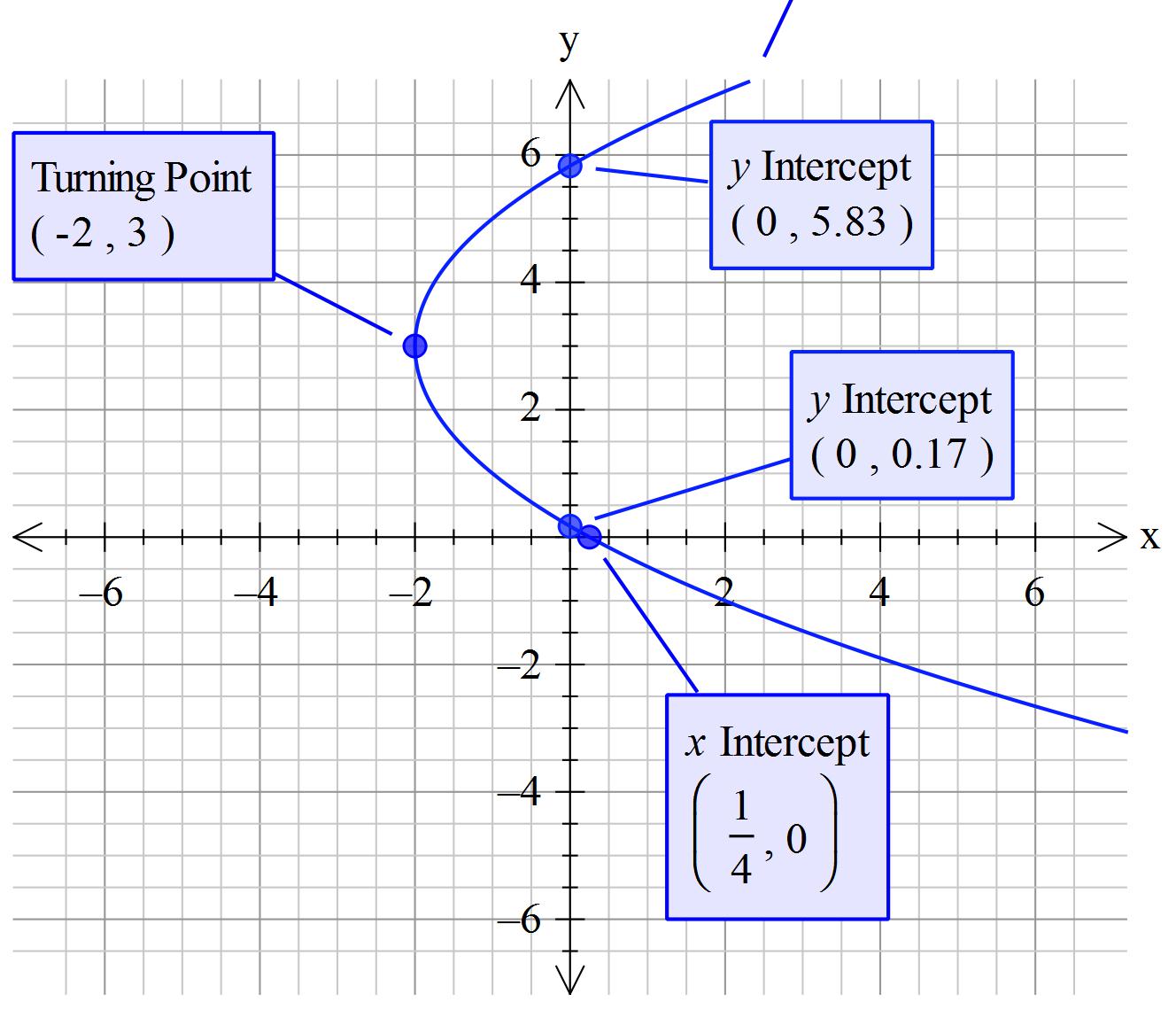
The structure of this is such that it implies #f(y)# instead of #f(x)# so that is how I am going to treat it. The consequence is that it rotates an #f(x)# graph so that the axis of symmetry is parallel to the x-axis instead of the y-axis.
Write as:
#" "4x=y^2-6y+1#
Divide both sides by 4
#" "x=1/4 y^2-6/4y+1/4#
#color(blue)("Determine the vertex")#
Write as:
#" "x=1/4(y^2-6y)+1/4#
#y_("vertex")=(-1/2)xx(-6) = +3#
#x_("vertex")=1/4(3)^2-3/2(3)+1/4" "=" "-2#
#color(blue)("Vertex "->(x,y)->(-2,3)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine "x" intercept")#
Set #y=0#
#color(blue)(=> x_("intercept")=1/4(0)^2-3/2(0)+1/4)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine "y" intercept")#
Set #x=0#
#=>1/4(y^2-6y)+1/4=0#
#color(brown)("Completing the square")#
#1/4(y-3)^2+1/4 +k=0#
Where #k# is the constant of correction.
#k=(-1)xx[1/4(-3)^2] = -9/4# giving:
#color(brown)(1/4(y-3)^2+1/4 +k=0)color(blue)(" "->" "1/4(y-3)^2-2=0#
'....................................................................
#=>(y-3)^2=8#
#y-3=+-sqrt(8)" "=+-2sqrt(2)#
#y_("intercept")=3+-2sqrt(2)#
#color(blue)(y_("intercepts")~~5.828" and "0.172" to 3 decimal places")#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~