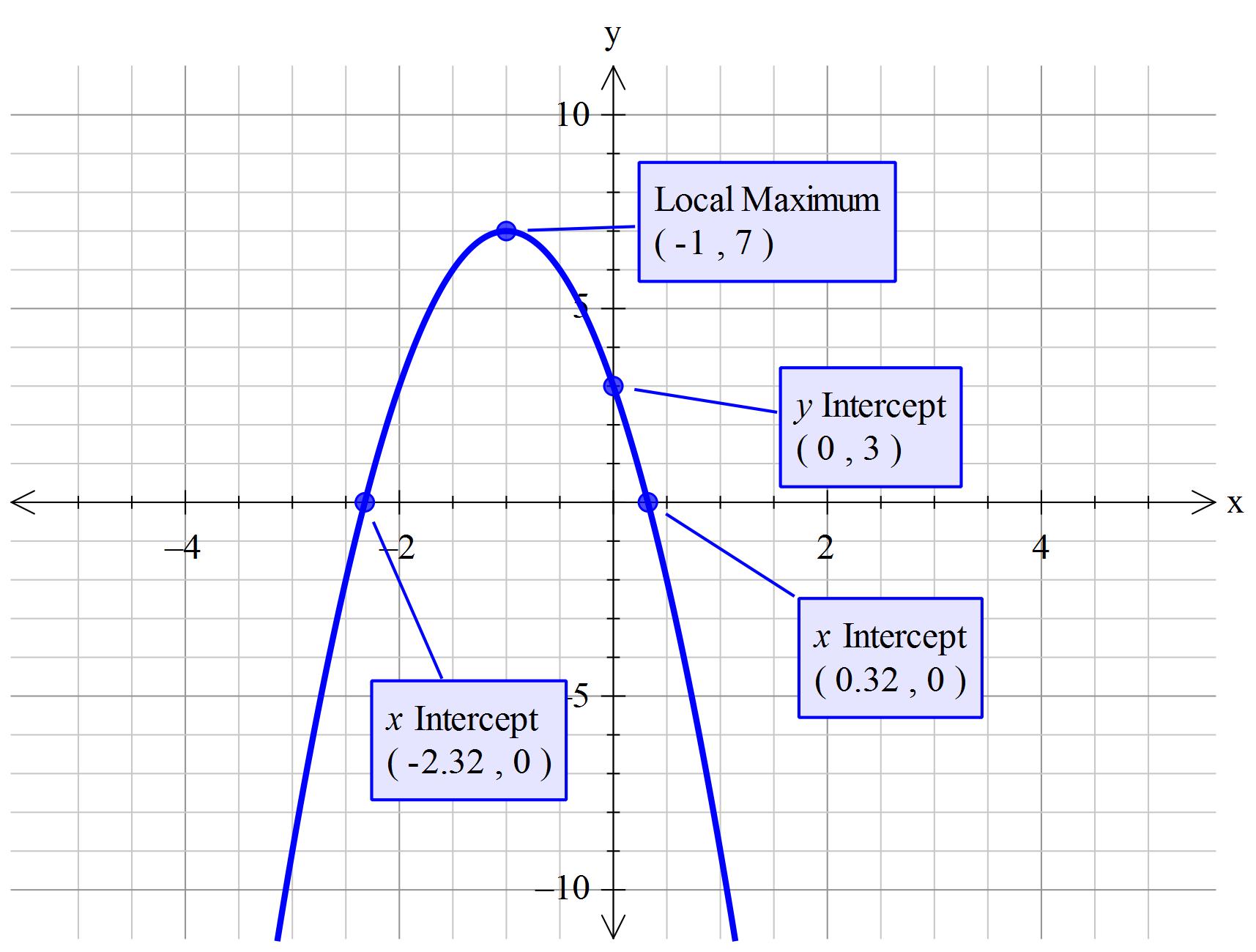
Given:#" "y=-4x^2-8x+3#
This equation does not have whole numbers as roots so the formula has to be used to solve for #x_("intercepts")#.
#color(blue)("Determine the y-intercept")#
#color(green)(y_("intercept") = "the constant "=3)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the vertex")#
Write the equation as:
#" "y=-4(x^2 +2x)+3->#part way to vertex form
Consider #2" from "2x#
Apply #(-1/2)xx2 = -1#
#color(blue)(x_("vertex")=-1)#
By substitution:
#color(green)(y_("vertex")=-4(-1)^2-8(-1)+3 = +7)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine "x_("intercepts"))#
Using: #y=ax^2+bx+c# where #" "a=-4"; " b=-8"; " c=3#
#" and "x=(-b+-sqrt(b^2-4ac))/(2a)#
#x=(+8+-sqrt((-8)^2-4(-4)(3)))/(2(-4)) #
#x=(+8+-sqrt(112))/(-8) #
#x=(8+-sqrt(2^2xx28))/-8#
#x=(8+-2sqrt(28))/-8#
#color(green)(x=-1+-sqrt(28)/4 ~~0.3229" or "x~~ -2.3229)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~