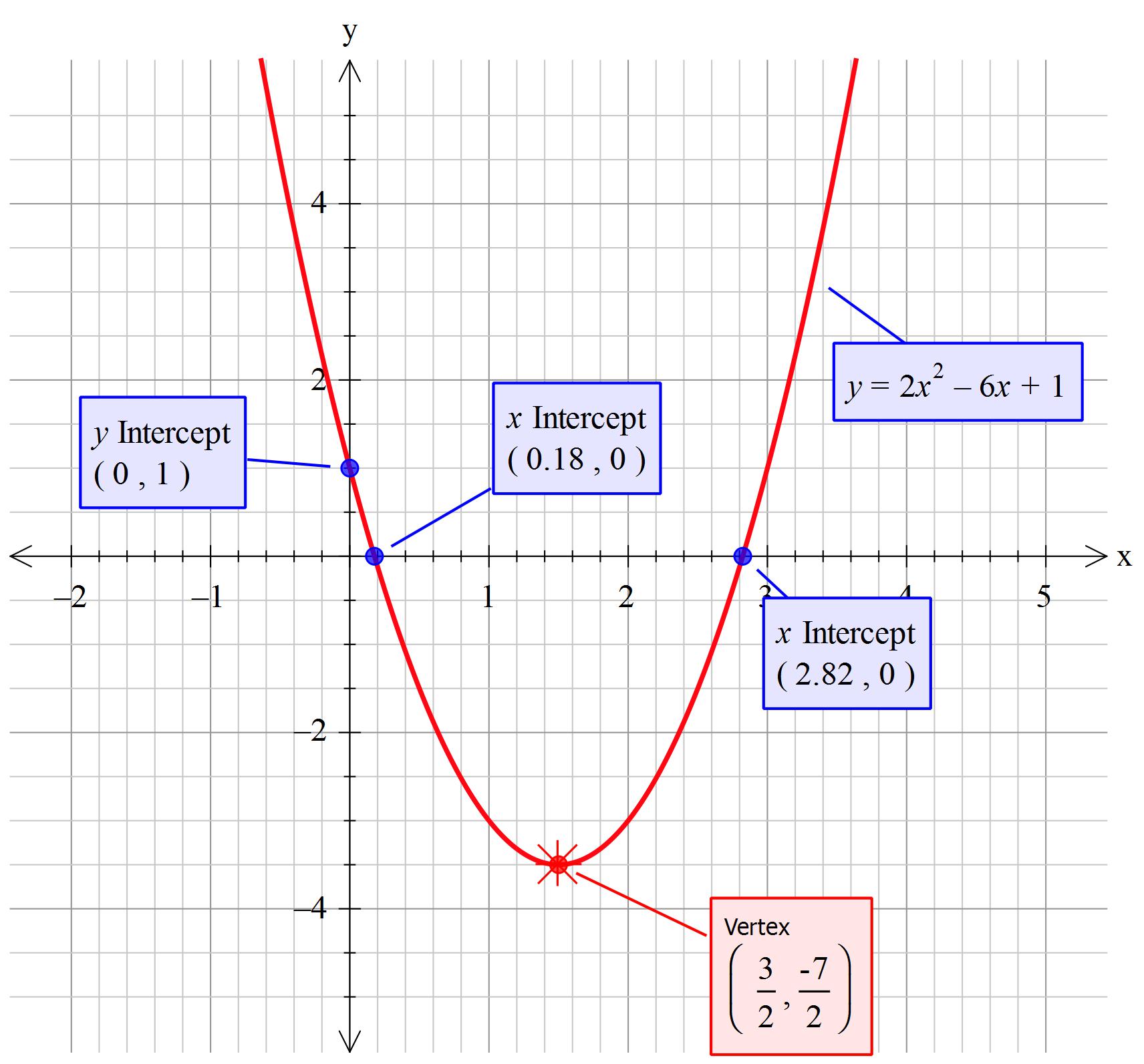
#color(blue)("A little bit of a cheat type approach")#
#color(red)("Straight off: the intercept is the same as the constant +1")#
There is a quick trick to finding #x_("vertex")# and hence #y_("vertex")#
write as #y=2(x^2-3x)+1#
#x_("vertex")=(-1/2)xx(-3) = +3/2#
#=>y_("vertex")=2(3/2)^2-6(3/2)+1 = -3 1/2#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("More formal type solution for vertex - Shortcut")#
Changing it one step at a time. With practice you would do this in perhaps 4 lines.
Convert to vertex form equation
#color(red)("Step 1") #
Write as #y=2(x^2-3x)+1 + k#
where #k# is a correction for an error that is about to be introduced. To be mathematically correct, its value changes at each modification stage but is only taken notice of at the end.
,.........................................................................................
#color(red)("Step 2")#
For the #3x# halve the three and remove the #x#
#y=2(x^2-3/2)+1+k larr" now "k" starts to be applied"#
,...........................................................................................
#color(red)("Step 3")#
Move the power from #x^2# to outside the brackets.
#y=2(x-3/2)^2+1+k#
,.........................................................................
#color(red)("Step 4")#
#color(magenta)("The error comes from the")#
#color(magenta)(2xx (-3/2)^2) # in
#y=color(magenta)(2)(xcolor(magenta)(-3/2))^(color(magenta)(2)) #
So #" "2(-3/2)^2+k=0 larr# the correction process
#=> k=-2(-3/2)^2 = -cancel(2)^1xx9/(cancel(4)^2) =-9/2 #
So we finally have
#color(brown)(y=2(x-3/2)^2+1+k ->color(blue)(-> y=2(x-3/2)^2+1-9/2#
#color(green)(y=2(x-3/2)^2-7/2#
#color(red)("Vertex "->(x,y)->(-1xx-3/2,-7/2) = (3/2,-7/2))#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)(" Determine x-intercepts")#
Write as #2(x-3/2)^2=7/2" "->(x-3/2)^2=7/4#
Take the square root of both sides
#x-3/2=+-sqrt(7/4) = +-sqrt(7)/2#
#x=+3/2+-sqrt(7)/2#
#color(red)(x=+2.822 and +0.177)#