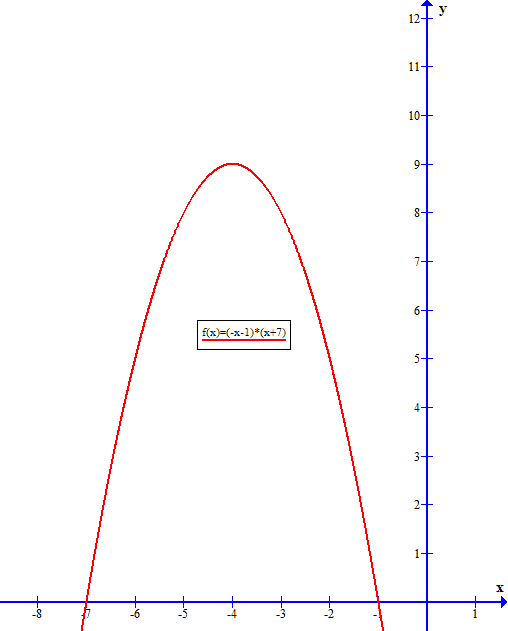
How do you find the vertex and intercepts for #y=(-x-1)(x+7)#?
1 Answer
vertex at:
Explanation:
Given
The y-intercept is the value of
Substituting
The y-intercept is at
The x-intercepts are the values of
The x-intercepts are at
The vertex can be determined in a couple ways:
1. by converting the given equation into vertex form (ask if you need to see this version)
or
2. by noting that the axis of symmetry will cross the X-axis a t he mid point between the 2 x-intercepts;
namely at
Substituting
So the vertex is at