Question

How do you find the vertex and intercepts for `y = (x + 3)^2 – 4`?

Answer 1

Vertex `->(x,y)=(-3,-4)`
`x_("intercepts")->(x,y) = (-5,0) and (-1,0)`
`y_("intercept")->(x,y)=(0, 5)`

Explanation:

`color(blue)("Determine the "x" intercepts")`

Set `y=0=(x+3)^2-4`

Add 4 to both sides

`4=(x+3)^2`

Square root both sides

`+-2=x+3`

Subtract 3 from both sides

`x=-3+-2`

`x_("intercepts")->(x,y) = (-5,0) and (-1,0)`

You may if you so choose determine the vertex from this point

`x_("vertex")` is midway between the x intercepts then by substitution determine y. The method I used later takes less work.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Determin "y" intercept and vertex")`

Given `y(xcolor(magenta)(+3))^2color(green)(-4)`

`x_("vertex")=(-1)xx(color(magenta)(+3))=-3`
`y_("vertex")=color(green)(-4)`

Vertex `->(x,y)=(-3,-4)`

`y_("intercept")=color(magenta)(+3)^2color(green)(-4) = 5`

Answer 2

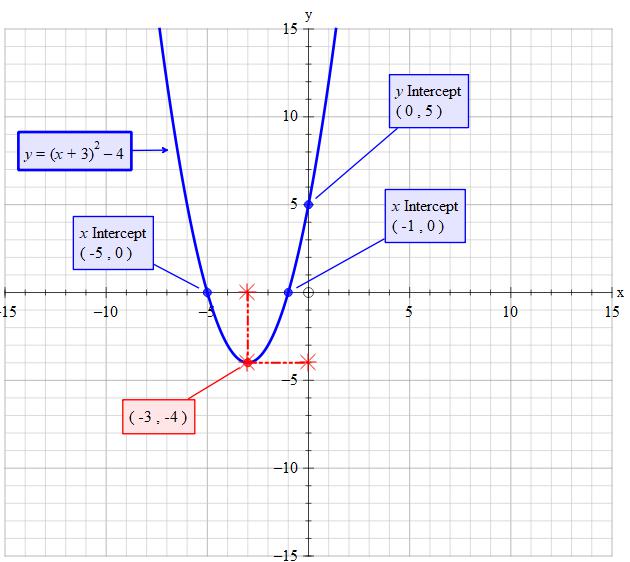
Vertex is at `(-3, -4)` , y intercept is `y=5 or (0,5)`
x intercepts are at `(-1,0) and (-5,0)`

Explanation:

`y=(x+3)^2-4`

Comparing with vertex form of equation

`f(x) = a(x-h)^2+k ; (h,k)` being vertex we find

here `h=-3 , k=-4 :.` Vertex is at `(-3, -4)`

y intercept is found by putting `x=0` in the equation

`y = (x+3)^2-4 :. y=(0+3)^2-4 =9-4=5`

So y intercept is `y=5 or (0,5)`

x intercepts are found by putting `y=0` in the equation

`y = (x+3)^2-4 :. 0=(x+3)^2-4` or

`(x+3)^2=4 or (x+3) =+-sqrt4 or (x+3) =+-2`

`:. x=-3+-2 :. x=-1 and x=-5`

x intercepts are at `(-1,0) and (-5,0)`

graph{(x+3)^2-4 [-10, 10, -5, 5]} [Ans]

Answer 3

Vertex = `(-3,-4)`

y-intercept = `(0,5)`

x-intercepts = `(-1,0)` and `(-5,0)`

Explanation:

First, expand `y=(x+3)^2-4` into `y=x^2+6x+5`.

The x-vertex of a quadratic equation `y=ax^2+bx+c` is given by `-b/2a`.

Plugging in `a=1`, `b=6`, and `c=5`, we find that the x-vertex is `-6/2=-3`.

Now we plug in `x=-3` into `y=x^2+6x+5` to get the y-vertex, which is `-4`.

So our vertex is `(-3,-4)`.

To find the y-intercept of a quadratic equation, plug in `0` for the x value, and you will get `5`.

To find the x-intercept of a quadratic equation, plug in `0` for the y value, and you will get two solutions, `x=-1` and `x=-5`.

So our y-intercept is `(0,5)`, and our x-intercepts are `(-1,0)` and `(-5,0)`.