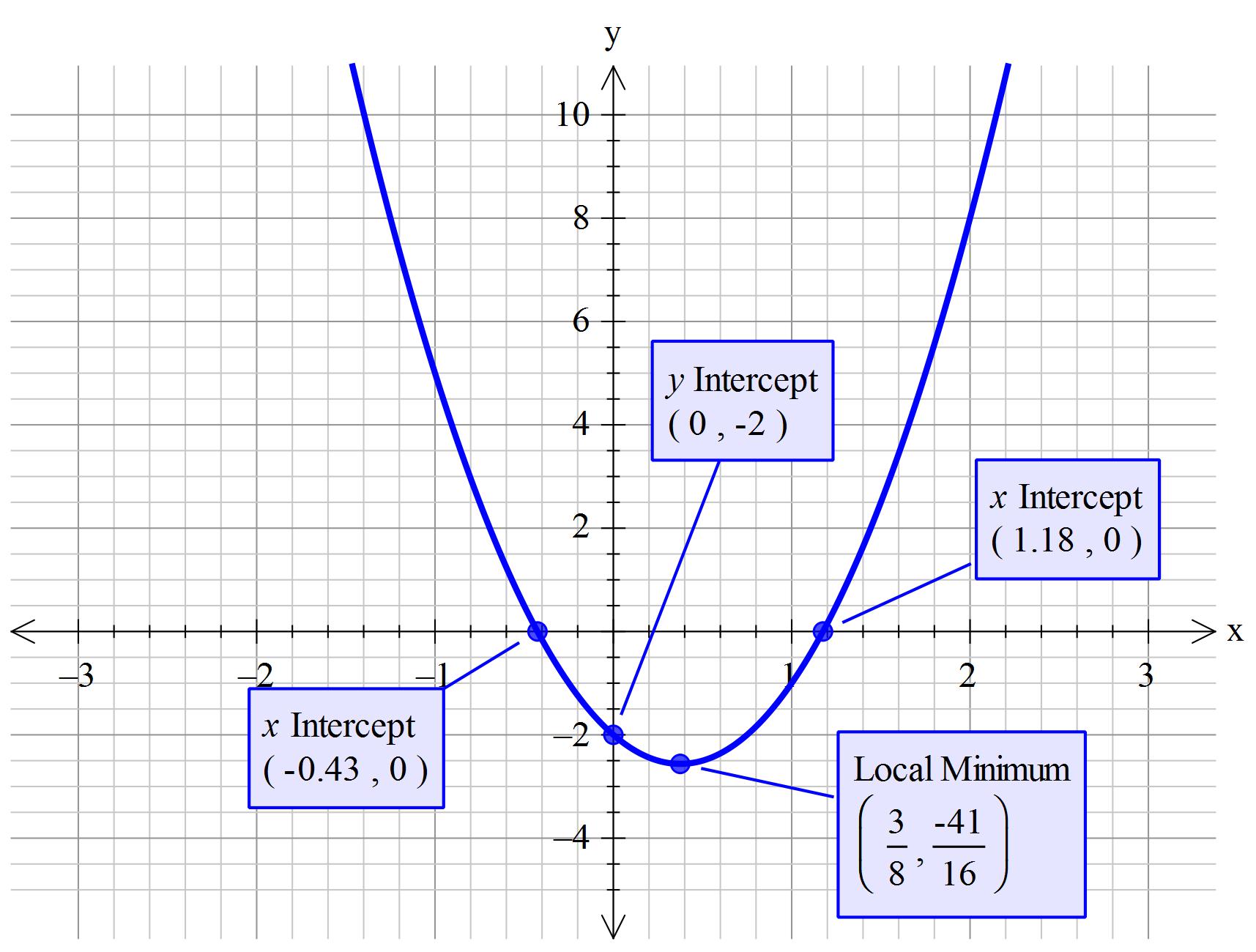
How do you find the vertex and the intercepts for # 4x^2 - 3x - 2 = 0#?
1 Answer
Explanation:
There is a really cool way to find the axis of symmetry and hence
Write the given equation as:
Now consider the
Apply:
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Substitute
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The graph will cross the y-axis at x=0 so by substitution.
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
There are not whole number factors for this equation so we are forced to use the equation method.
Where
and:
23 is a prime number so you can not do any more with it. So if you whish have a precise solution there is no choice other than to state:
You could work out the decimals if you wish but these will not be precise!
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~