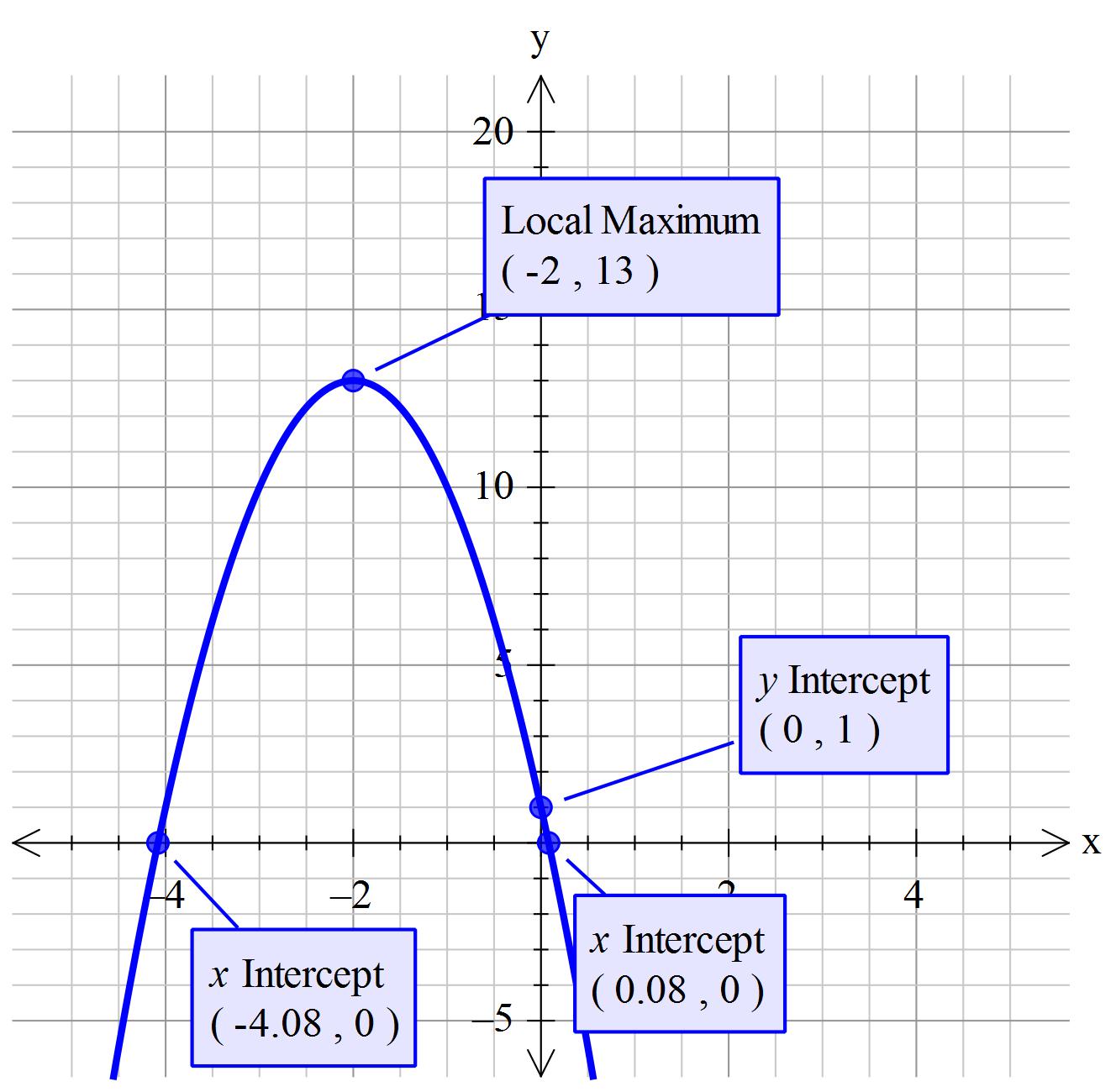
I much prefer the format:
#f(x)=-3x^3-12x+1#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Straight off, the "y_("intercept")" is the constant of +1")#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Write as #y=-3(x^3+12/3 x) +1#
#color(blue)(x_("vertex") = (-1/2)xx(+12/3) = -2)#
#color(brown)("By substitution of "x)#
#color(blue)(y_("vertex") =-3(-2)^2-12(-2)+1 = +13)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine x intercepts")#
This equation does not have whole number x intercepts
Set #0=-3x^2-12x+1#
Std form #-> y=ax^2+bx+c #
Where#" "x=(-b+-sqrt(b^2-4ac))/(2a)#
#=> x= (+12+-sqrt((-12)^2-4(-3)(1)))/(2(-3))#
#x= (12+-sqrt(156))/(-6)#
#x= -2+-sqrt(2^2xx39)/(-6)#
#x= -2+-sqrt(39)/(-3)#
'~~~~~~~~~~~~~~~~~~~~~~~
Consider: #color(blue)(x= -2-sqrt(39)/(-3) = +0.0817)# to 4 decimal places
Consider: #color(blue)(x= -2+sqrt(39)/(-3) = -4.0827)# to 4 decimal places