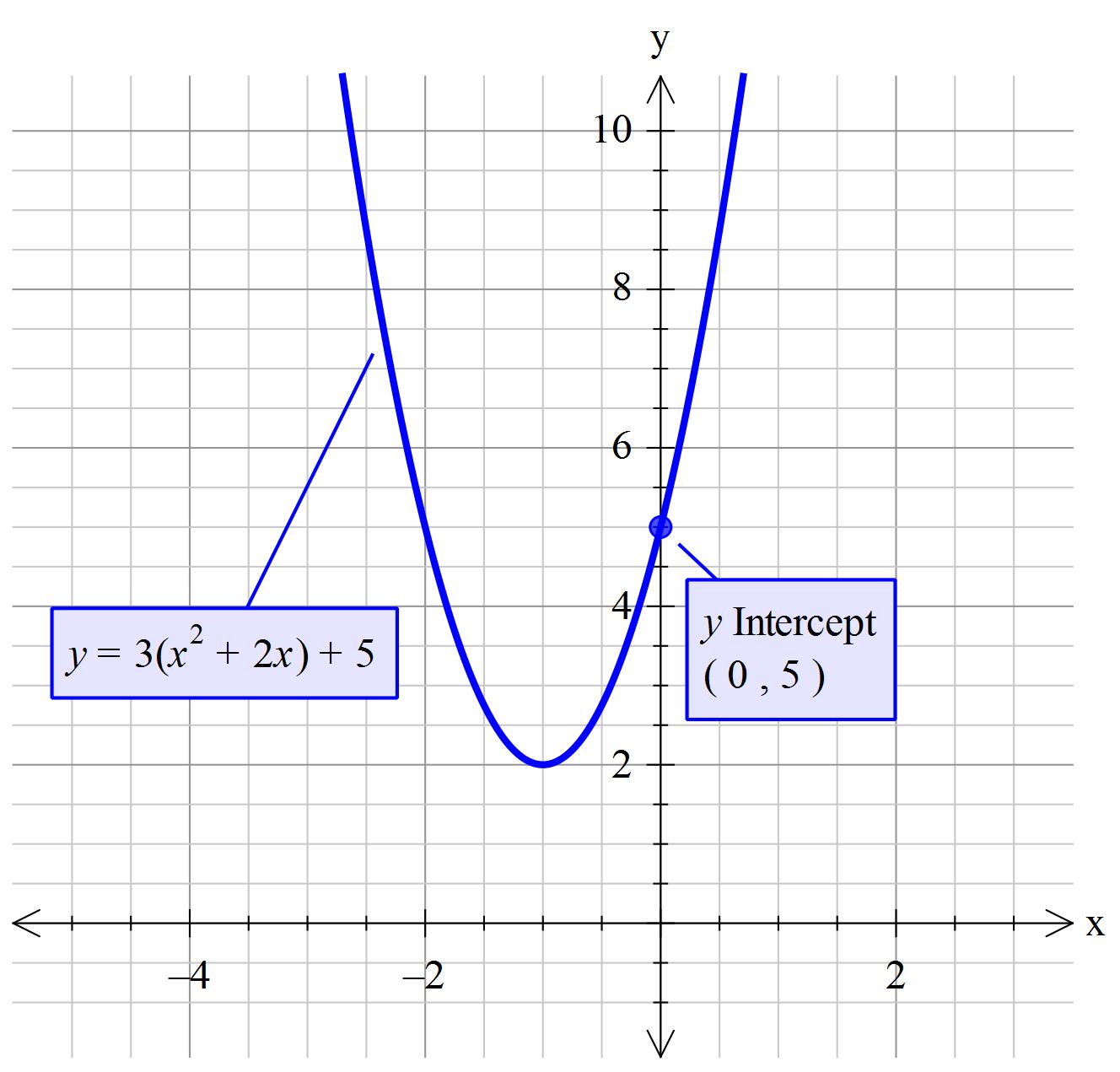
Given:#" "t(x)=3(x^2+2x)+5#
This is part way towards converting standard equation form to vertex form.
#color(blue)("Determine the y-intercept")#
The constant of 5 is the same as the constant #c# in #y=ax^2+bx+c# the y-intercept is #y=c=5#
#color(blue)(=> y_("intercept")->(x,y)->(0,5))#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the x-intercepts for " x in RR)#
First of all lets make sure they exist.
Consider the method of solving using the formula where
#x=(-b+-sqrt(b^2-4ac))/(2a)#
The part that is #sqrt(b^2-4ac)# is called the determinant.
From #sqrt(b^2-4ac)" ; if "b^2-4ac < 0# then there are no x-intercepts in the 'set' of numbers that are called 'Real'. However there are solutions that are in the 'set' of numbers called 'Complex'.
#color(brown)(y=ax^2+bx+c)color(blue)(" "->" "y= 3x^2+6x+5)#
#color(brown)(=>sqrt(b^2-4ac)color(blue)(" "->" "sqrt(6^2-4(3)(5))#
#sqrt(36-60)# and #36-60<0#
#color(blue)("Thus "x_("intercept") !in RR)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Slightly higher level of mathematics
#color(blue)("Determine the x-intercepts for " x in CC " (complex numbers)")#
Completing the square gives:
Standard form#" "y=ax^2+bx+c" "->" "y=3x^2+6x+5#
#" " ->" "a(x+b/(2a))^2+c+k#
#t(x)=3(x^2+2x)+5" " ->" "t(x)=3(x+1)^2+5+k#
where #k=(-1)xxa(b/(2a))^2#
#k=(-1)xx(3xx1^2) =-3#
#=> t(x)=3(x+1)^2+2#
Set to zero
#=> 0 = 3(x+1)^2+2#
#(x+1)^2=-2/3#
#x=+-sqrt(-1xx2/3)color(white)(.)-1#
#x=-1+-sqrt(2/3)color(white)(..)( i)#
But #sqrt(2/3)=sqrt(6)/3#
#color(blue)(x=-1+-sqrt(6)/3color(white)(..)i#