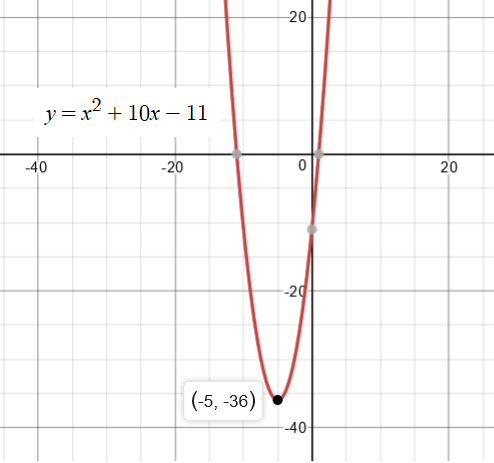
How do you find the vertex of a parabola #f(x)=x^2 +10x-11#?
1 Answer
Mar 23, 2018
Vertex of the parabola is at :
Explanation:
The Standard form for the quadratic equation is :
Given:
where
Find the x-coordinate of the vertex using the formula
To find the y-coordinate value of the vertex, set
Simplify the right-hand side.
Hence,
Vertex of the parabola is at :
Also observe that, since the coefficient of
Please refer to the image of the graph below: