How do you find the vertex of y=2x^2-4xy=2x2−4x?
2 Answers
Vertex
Explanation:
Given -
y=2x^2-4xy=2x2−4x
x=(-b)/(2xxa)=(-(-4))/(2 xx 2)=4/4=1x=−b2×a=−(−4)2×2=44=1
At
Vertex
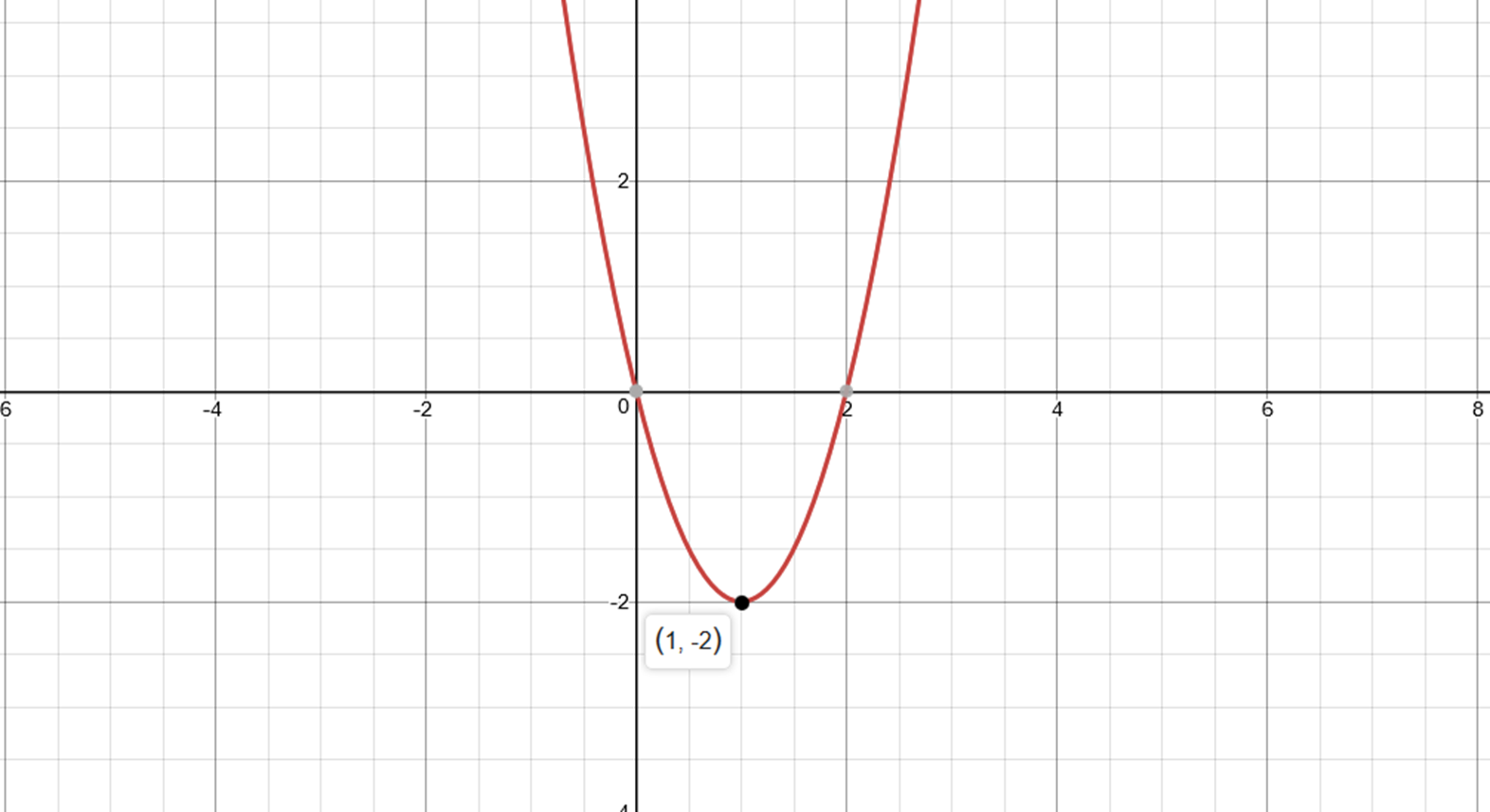
The vertex is at
Explanation:
This quadratic equation is in standard form, or
We know that
To find the vertex in a standard quadratic equation, we have to do two things.
Therefore, our vertex is at
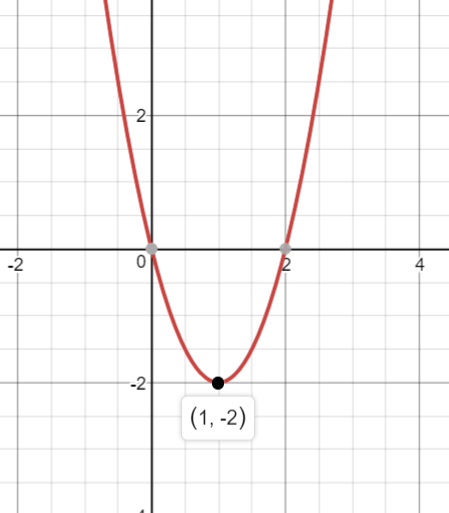
(desmos.com)
As you can see, the vertex is indeed at
For more help with finding the vertex from the standard equation, feel free to watch this video:
Hope this helps!


