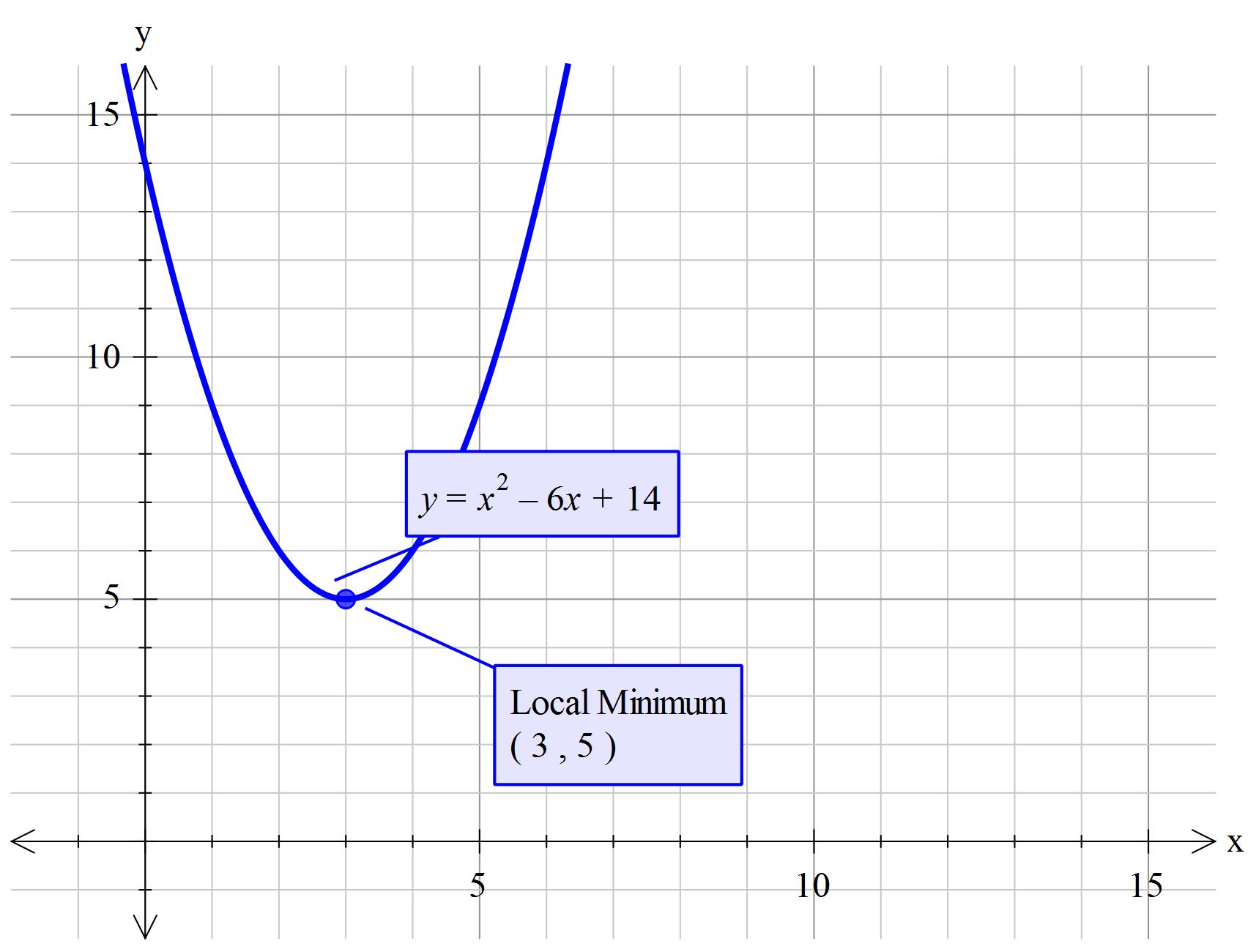
How do you find the vertex of #y= x^2 - 6x + 14#?
1 Answer
Mar 19, 2016
Vertex
Explanation:
The question does not define the method to be used so you have freedom of choice.
Let me show you a 'sort of' cheat method. Actually it forms part completing the square but does not take to the end of the process.
Consider standard form
Write this as:
Then you have
For this question:
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
By substitution
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~