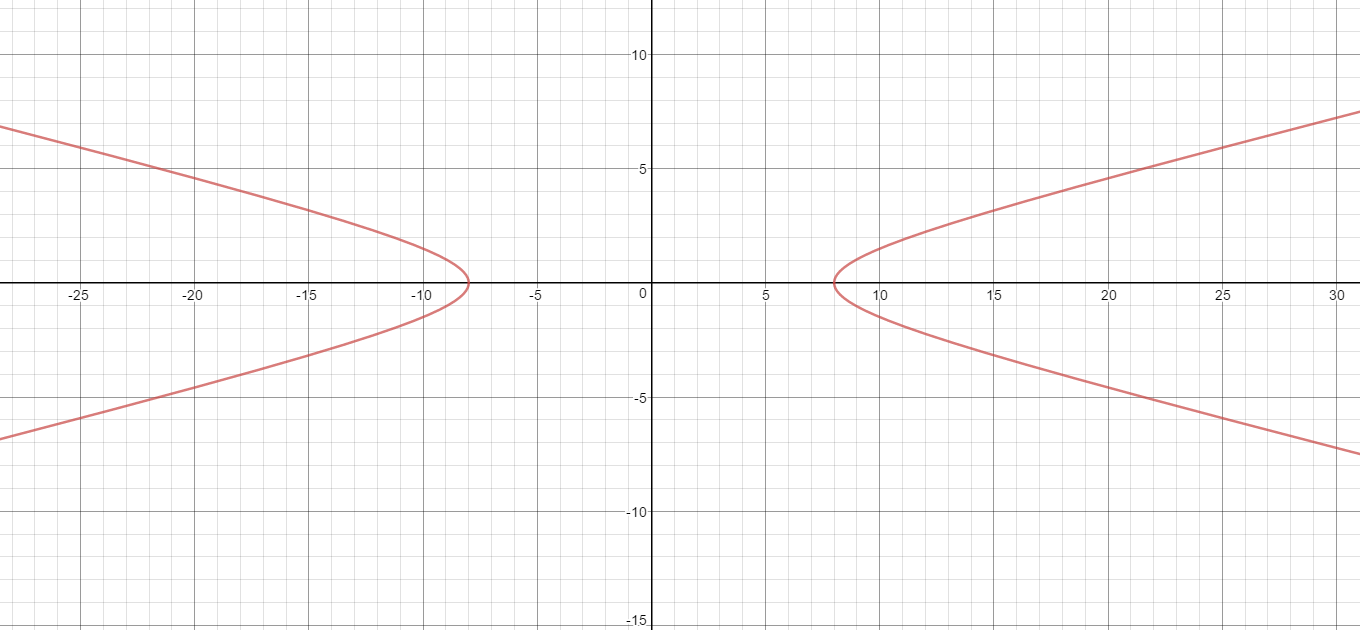
How do you find the vertices, asymptote, foci and graph #x^2/64-(9y^2)/4=1#?
1 Answer
Dec 6, 2016
Please see the explanation.
Explanation:
Standard form for a Hyperbola of this type (Horizontal Transverse Axis) is:
The center is at:
The vertices are at:
The foci are at:
The asymptotes are:
Let put the given equation in standard form:
The center is at:
The vertices are at:
The foci are at:
The asymptotes are:
Graph: