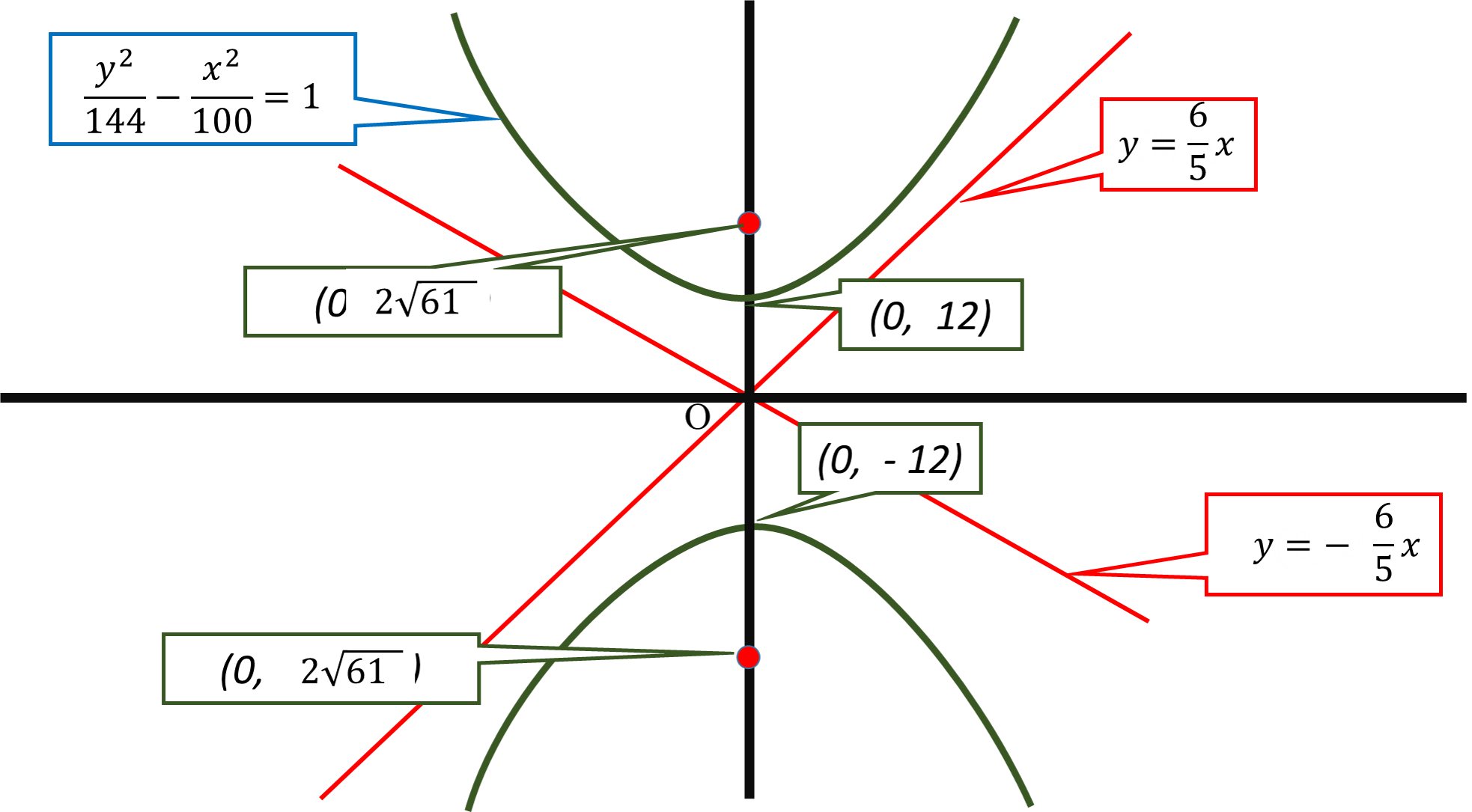
How do you find the vertices, asymptote, foci and graph #y^2/144-x^2/100=1#?

Question

2046 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-10-22T08:17:52

#y=6/5x#
#y=-6/5x#
Foci

#(0, 2sqrt61)#
#(0, -2sqrt61)#

vertices

#(0, 12)#
#(0, -12)#

Given -

#y^2/144-x^2/100=1#

It is in the form

#y^2/b^2-x^2/a^2=1#

In this case

Asymptotes are

#y=b/a x#

#y=-b/a x#

When #x^2/a^2#is negative hyperbola opens up and down along the Y-axis

Vertices are

#(0, b)#

#(0, -b)#

Foci are -

#(0, c)#

#(0, -c)#

Let us apply this in our problem -

#a^2=100#
#a=+-sqrt100=+-10#
#b^2=144#
#b=+-sqrt144=+-12#
#c=sqrt(a^2+b^2)=sqrt(100+144)=sqrt244=sqrt(4*61)=+-2*sqrt61#
#c=+-2sqrt61#

Asymptotes

#y=+-12/10x=+-6/5x#

#y=6/5x#
#y=-6/5x#

Foci

#(0, 2sqrt61)#
#(0, -2sqrt61)#

vertices

#(0, 12)#
#(0, -12)#

enter image source here