Question

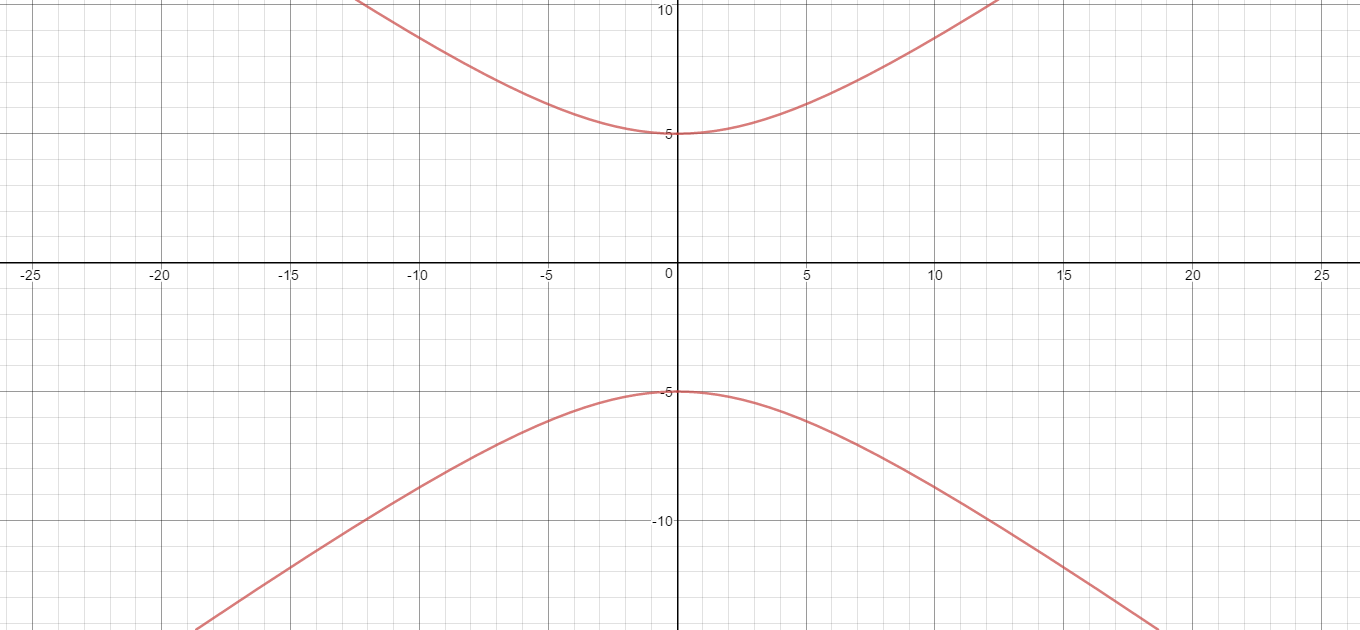
How do you find the vertices, asymptote, foci and graph `y^2/25-x^2/49=1`?

Answer 1

Please read this reference and the explanation.

Explanation:

The standard form for the equation of a hyperbola with a vertical transverse axis is:

`(y - k)^2/a^2 - (x - h)^2/b^2 = 1`

The center is: `(h, k)`
The vertices are: `(h, k - a) and (h, k + a)`
The foci are: `(h, k - sqrt(a^2 + b^2)) and (h, k + sqrt(a^2 + b^2))`
The equations of the asymptotes are:
`y = -a/b(x - h) + k and y = a/b(x - h) + k`

Write the given equation in this form:

`(y - 0)^2/5^2 - (x - 0)^2/7^2 = 1`

The center is: `(0, 0)`
The vertices are: `(0, -5) and (0, 5)`
The foci are: `(0, -sqrt(74)) and (0,sqrt(74))`
The equations of the asymptotes are:
`y = -5/7x and y = 5/7x`

Here is the graph: