Let's consider the right triangle with angle #x# where #cos(x) = sqrt(5)/6#
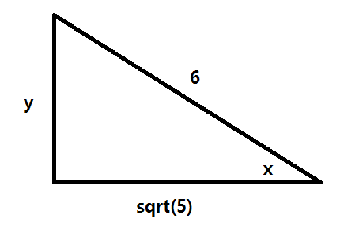
Then #cos^(-1)(sqrt(5)/6) = x# and so
#sin(cos^(-1)(sqrt(5)/6)) = sin(x) = y/6#
By the Pythagorean theorem,
#(sqrt(5))^2 + y^2 = 6^2 => y = sqrt(36 - 5) = sqrt(31)#
So we have one value of #sin(cos^(-1)(sqrt(5)/6))# as #sqrt(31)/6#
But assuming we are looking at #cos^(-1)# as multivalued, looking at it geometrically loses one solution, as we only look at one possibility for #cos^(-1)(sqrt(5)/6)#. To get the other, note that as as the cosine function is even,
#cos(-x) = cos(x) = sqrt(5)/6#
So we need to consider #-x# as our other value. Then, as the sine function is odd,
#sin(-x) = -sin(x) = -sqrt(31)/6#
Thus the two exact values of #sin(cos^(-1)(sqrt(5)/6))# are #sqrt(31)/6# and #-sqrt(31)/6#


