How do you find vertical, horizontal and oblique asymptotes for #(x^2 - 2x + 3) / x#?
1 Answer
Vertical asymptotes:
Vertical asymptotes occur when the denominator of a rational function equals to 0 (this being because division by 0 is undefined in mathematics). We can find any vertical asymptotes by setting the denominator to 0 and solving.
There will be a vertical asymptote at
Horizontal asymptotes:
Horizontal asymptotes only occur when the degree of the denominator is higher or equal to that of the numerator. We don't have this situation in our function.
Oblique asymptotes:
Oblique asymptotes occur when the denominator has a lower degree than the numerator. If the function is
Therefore, we will have to divide your rational function. A thorough understanding of division of polynomials is usually a pre-requisite to finding oblique asymptotes.
The quotient is therefore
There will therefore be an oblique asymptote at
Here is the graph of the function:
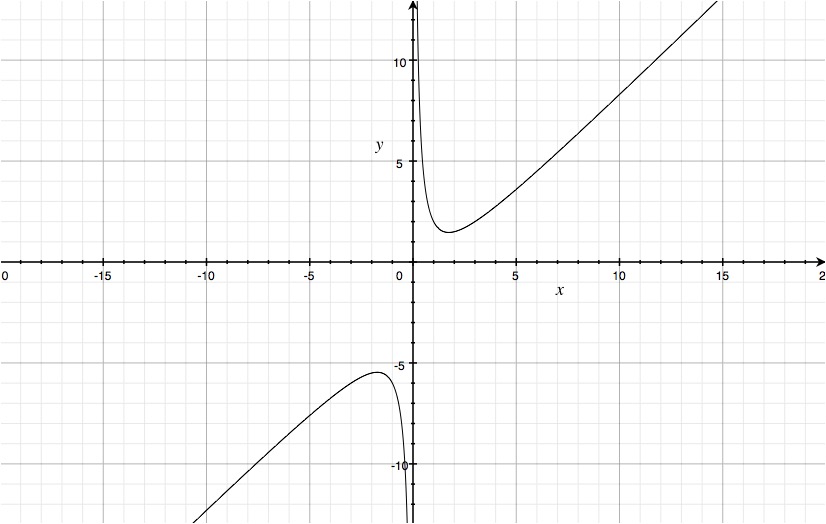
Hopefully this helps!

