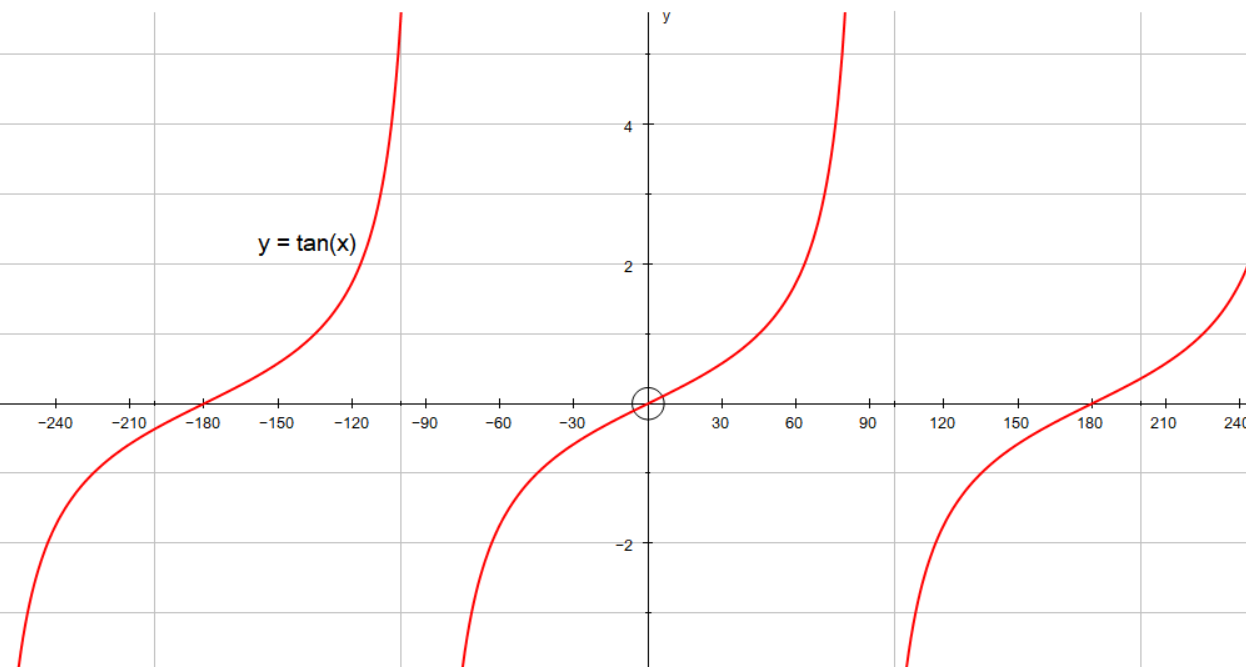
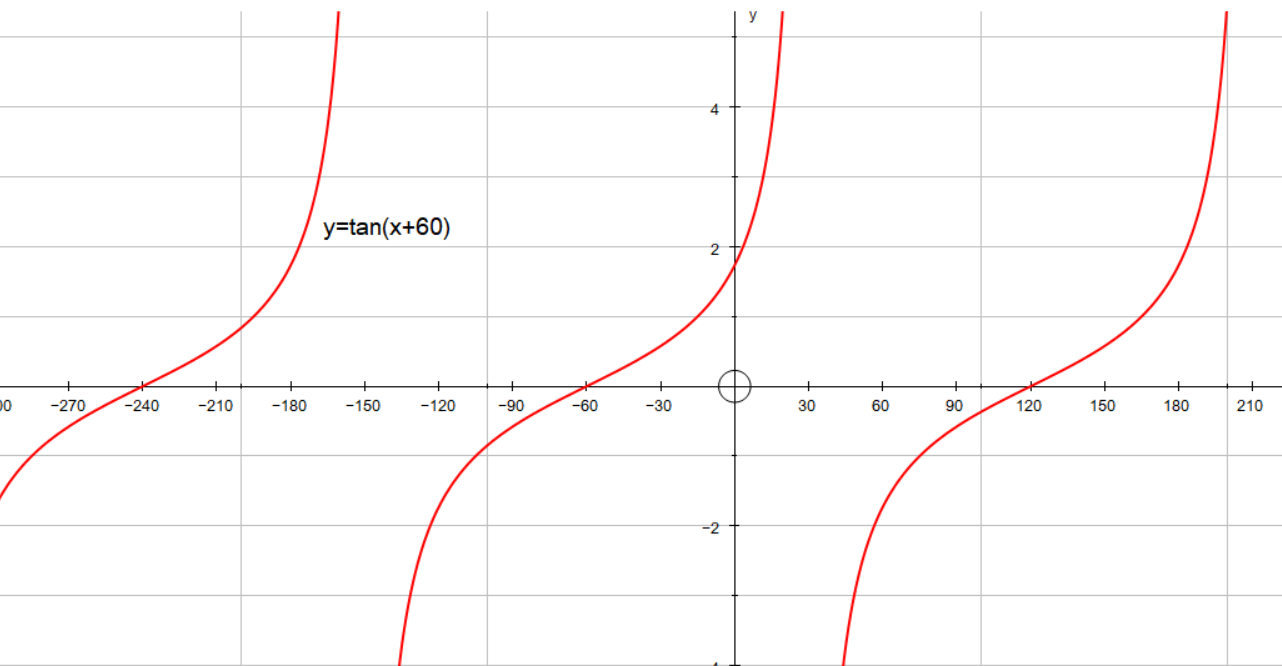
How do you graph and list the amplitude, period, phase shift for #y=tan(x+60)#?
1 Answer
Dec 18, 2017
See below.
Explanation:
If we look at a trigonometrical function written in the form:
We know that:
Amplitude = a
Period =
Phase shift =
Vertical shift = d
From example:
Amplitude ( see below)
period
period
Phase shift
This is the same as the graph of y = tan(x) translated 60 degrees in the negative x direction
Vertical shift
Amplitude can not be measured for the tangent function, because as:
as
Graphs: of