How do you graph and solve #2-x<=3-(5x-4)#?
1 Answer
The given inequality
can be simplified to
Explanation:
How do we graph and solve
We will try to simplify the inequality first before graphing:
Remove the parenthesis:
Combining like terms and simplifying:
Add
Rearrange the terms and simplify:
Subtract
Divide both sides of the inequality by
This is our simplified inequality.
We can graph this inequality as shown below:
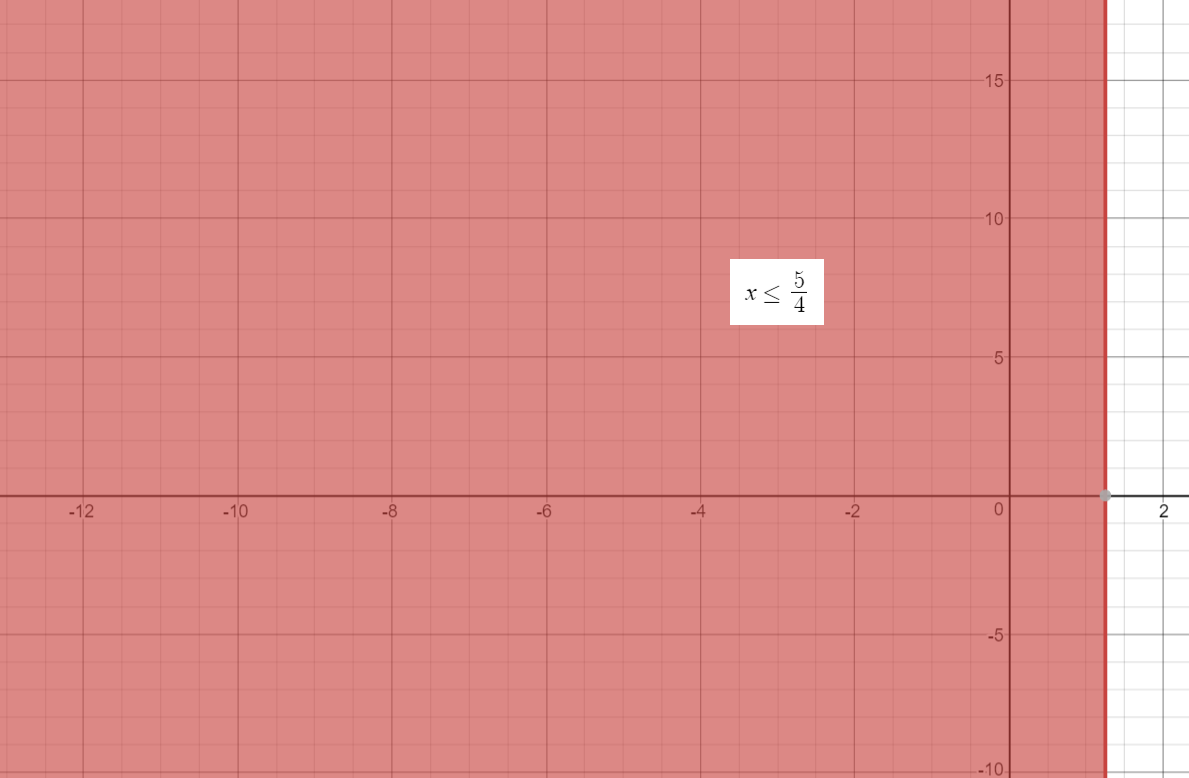
The solid line in the graph indicates the value
Hope it helps.

