Question

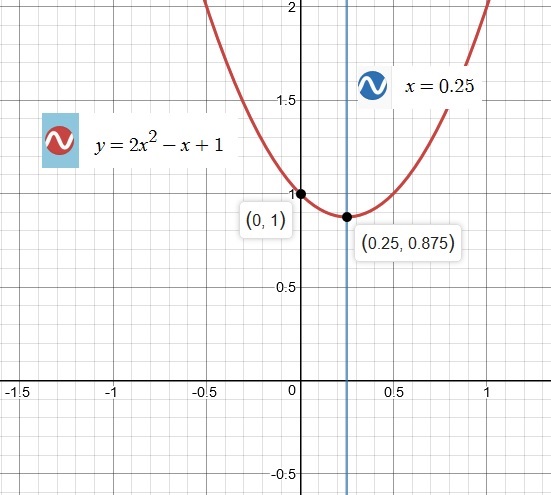
How do you graph `f(x)=2x^2-x+1` and identify the x intercepts, vertex?

Answer 1

See the explanation.

Explanation:

Given:

`color(red)(y=f(x)=2x^2-x+1)`

Our quadratic function is in Standard Form:

`color(blue)( y = f(x) = ax^2+bx+c`, where

`color(green)(a = 2; b=-1 and c=1)`

To find the Vertex, we can use the formula `color(red)([-b/(2a)]`

Hence,

Vertex = `color(red)([-b/(2a)]`

Vertex = `color(red)([-{(-1)/(2*2)}]`

Vertex = `color(red)(1/4 or 0.25}`

This is the x-coordinate value of our Vertex

To find the y-coordinate value of our Vertex,

substitute `color(blue)(x=0.25` in `color(red)(y=f(x)=2x^2-x+1)`

`y = 2*(0.25)^2-(0.25) + 1`

`y = 2*(0.625)-0.25+1`

`y = 0.125-0.25+1`

`y= 0.875`

Hence our Vertex can now be written as an Ordered Pair

Vertex = `color(blue)([0.25, 0.875]`

To find the x-intercepts we set `color(blue)((y=0)` and solve for `color(blue)x`

Hence, we have

`color(red)(y=2x^2-x+1=0)`

We will use the Quadratic Formula to solve for `x`:

`color(green)(x=[-b+- sqrt[b^2 - (4*a*c)]]/(2*a)`

`color(green)(a = 2; b=-1 and c=1)`

Substitute the values in our formula:

`x=[-(-1)+- sqrt[(-1)^2 - (4*2*1)]]/(2*2)`

Simplify to get

`x = 1+-sqrt(-7)/4`

We observe that there are No Real Solutions

Hence, the function does not have x-intercepts.

Additional point of information:

`color(blue)(x=0.25` is known as the Axis of Symmetry

What is the Axis of Symmetry?

The two sides of a graph on either side of the axis of symmetry look like mirror images of each other.

Next analyze the graph below to study the behavior of `f(x)`