#" "#
Given the exponential function: #color(red)(f(x)=3^(x-2)#
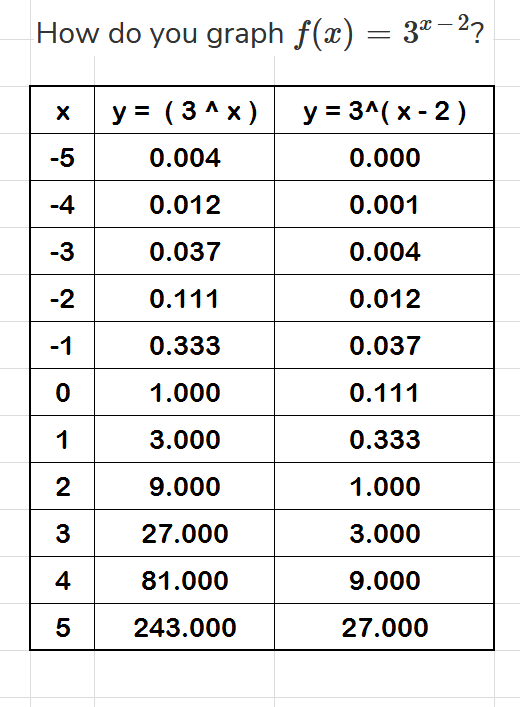
Before graphing this function, create a data table:
The table should contain values for #color(red)(x#, corresponding values for #color(red)(y=3^x) and color(red)(y=3^(x-2)#
We include the base function: #color(red)(y=3^x#, since it provides an opportunity to examine the behavior of both the graphs by comparing them.
The table shows #color(red)x# and the corresponding #color(red)(y# values:
Construct both the graphs:
#color(green)"Graph 1:"#
#color(blue)("Graph of "y = f(x) = 3^x#
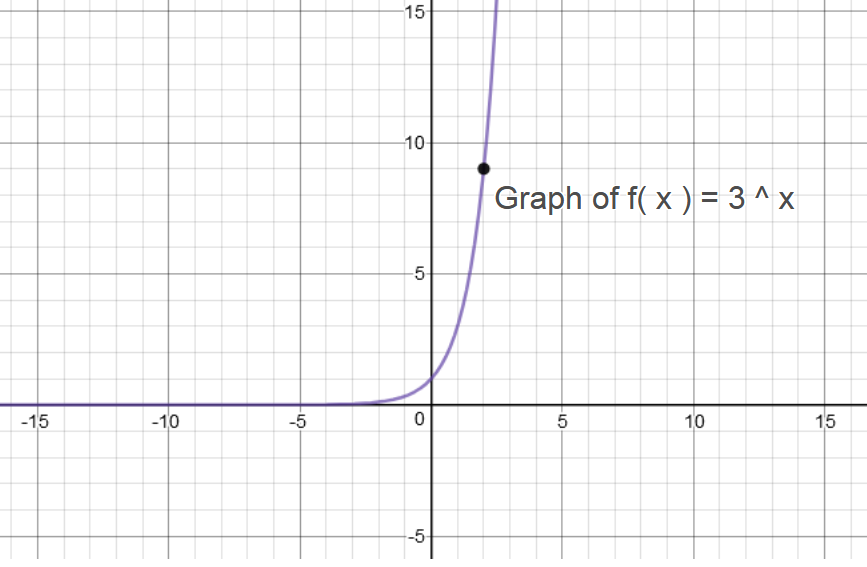
Domain : #(-oo, oo)#
Range : #(0, oo)#
y-intercept : #(0,1)#
Horizontal Asymptote :#y=0#
#color(green)"Graph 2:"#
#color(blue)("Graph of "y = f(x) = 3^(x-2#
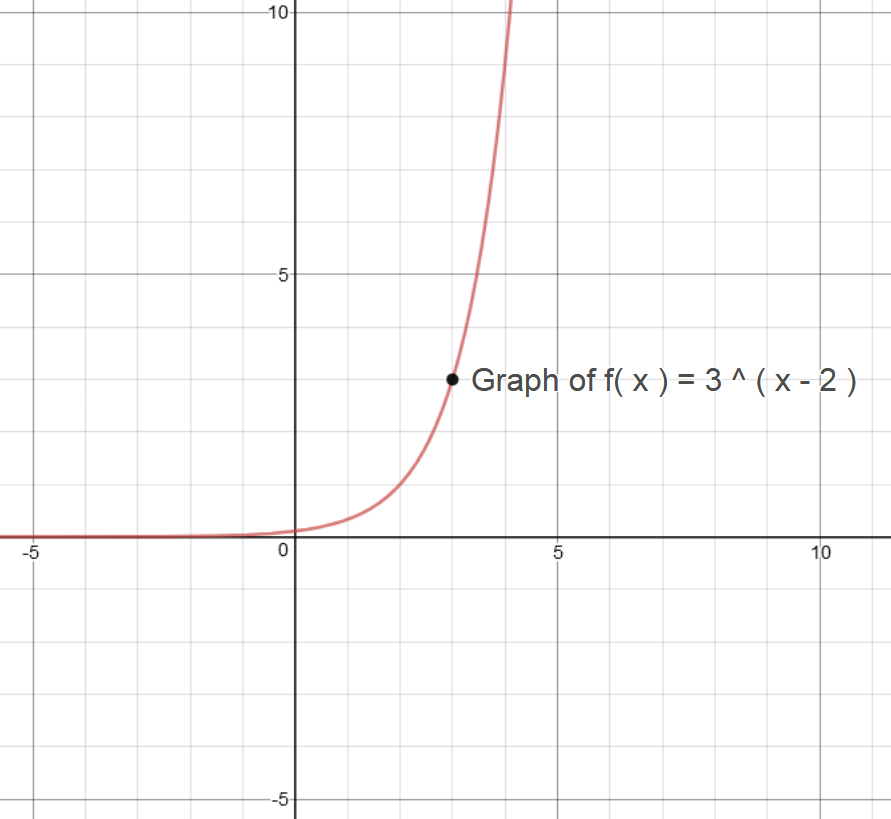
Domain : #(-oo, oo)#
Range : #(0, oo)#
y-intercept : #(0,1/0)#
Horizontal Asymptote :#y=0#
#color(green)"Graph 3:"#
#color(blue)("Graph of "y = f(x) = 3^(x) and y = f(x) = 3^(x-2)#
Compare the behavior of both graphs:
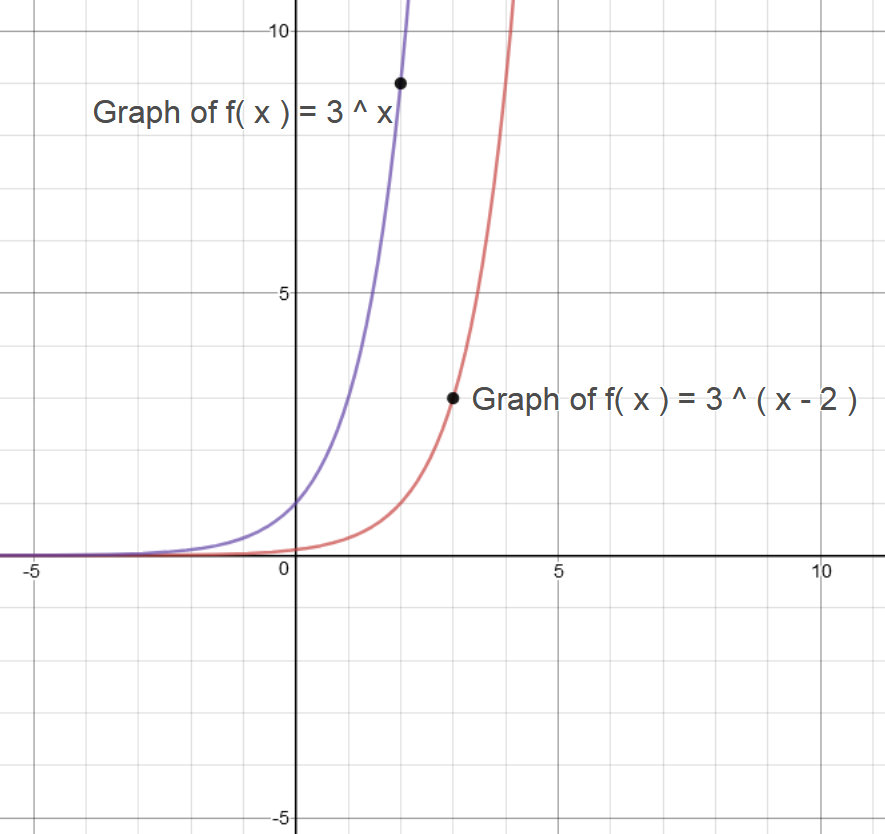
Translation is horizontal for #y = f(x) = 3^(x-2)# by #color(red)(2# units.
Hope it helps.





