First you need to be sure to avoid #x# values that makes the argument of your square root negative (you cannot find a real solution of a negative square root). So you set:
#4-x^2>=0# and:
#(2-x)(2+x)>=0#
so:
#x>=-2#
#x<=2#
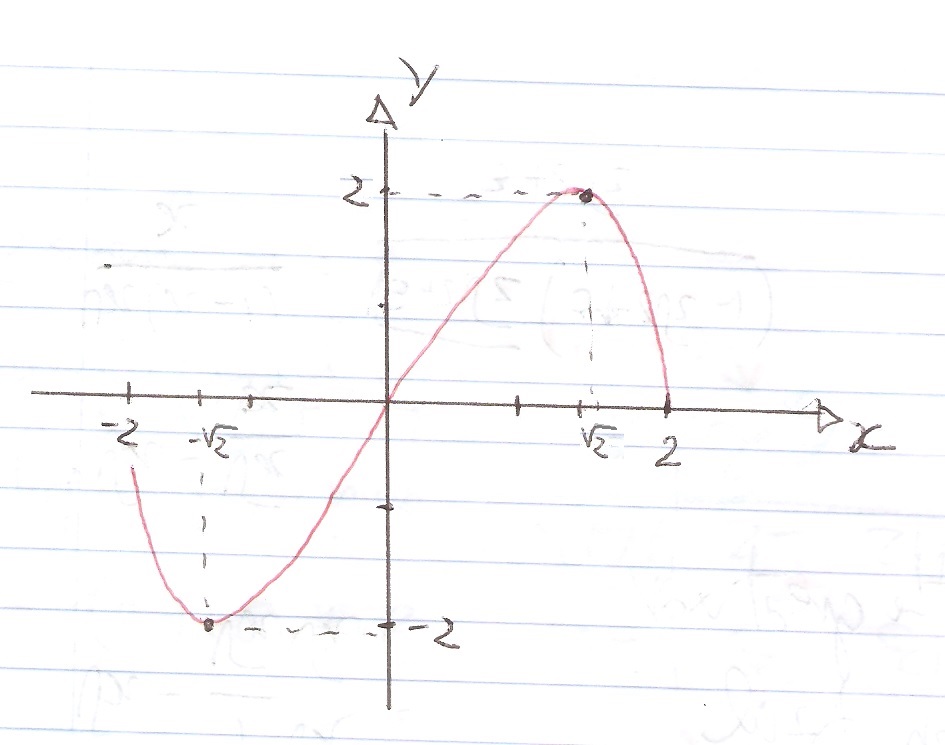
and #-2<=x<=2#
Outside this interval your function does not exist.
So, now we choose values for #x# and evaluate the correspondent #y#:
#x=2 => y=0#
#x=-2 => y=0#
#x=0 => y=0#
We have a graph that passes through #y=0# 3 times; probably our function changes quadrant in doing so.
For #x# approaching #-2# our function gives negative values (for example when #x=-1.9=> y=-1.2#) and when approaching #2# it has positive values (for example when #x=1.9=> y=1.2#). The graph of our function starts from #x=-2# going downwards, rises passing through #x=0# and then bends again to end up in #x=2#. I must have a minimum and a maximum somewhere.
I evaluate the derivative of the function and set it equal to zero to find these points:
#f'(x)=sqrt(4-x^2)-x^2/(sqrt(4-x^2))#
setting it equal to zero and manipulating it I got:
#4-2x^2=0# which gives #x=+-sqrt(2)#
so you get:
#x=-sqrt(2) => y=-2# minimum and
#x=sqrt(2) => y=2# maximum
Finally: