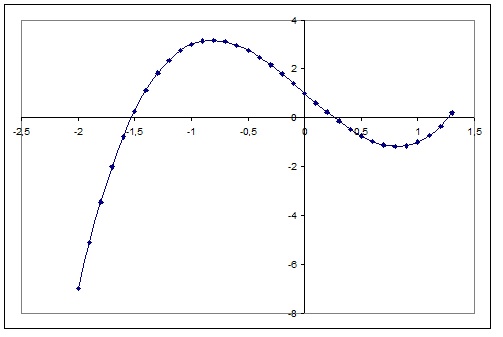
How do you graph #y = 2x^3 - 4x + 1# using the first and second derivative?
1 Answer
Feb 21, 2015
You can start by using the first derivative to find points of maximum and minimum:
You set the first derivative equal to zero:
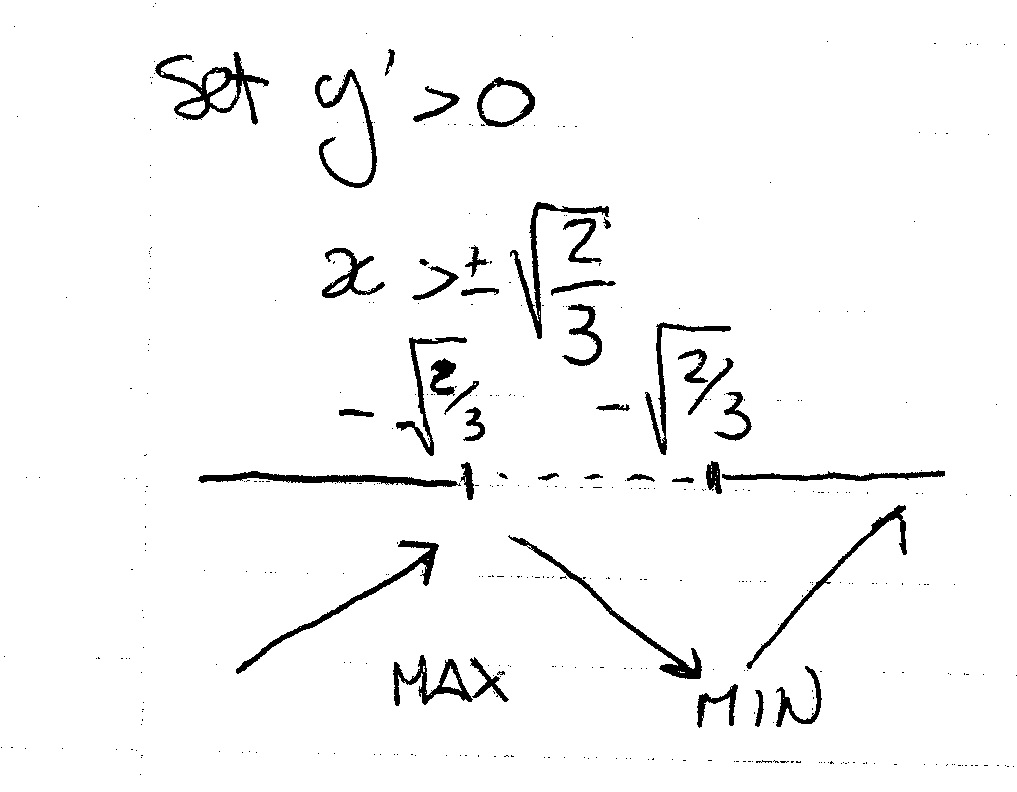
So:
maximum:
minimum:
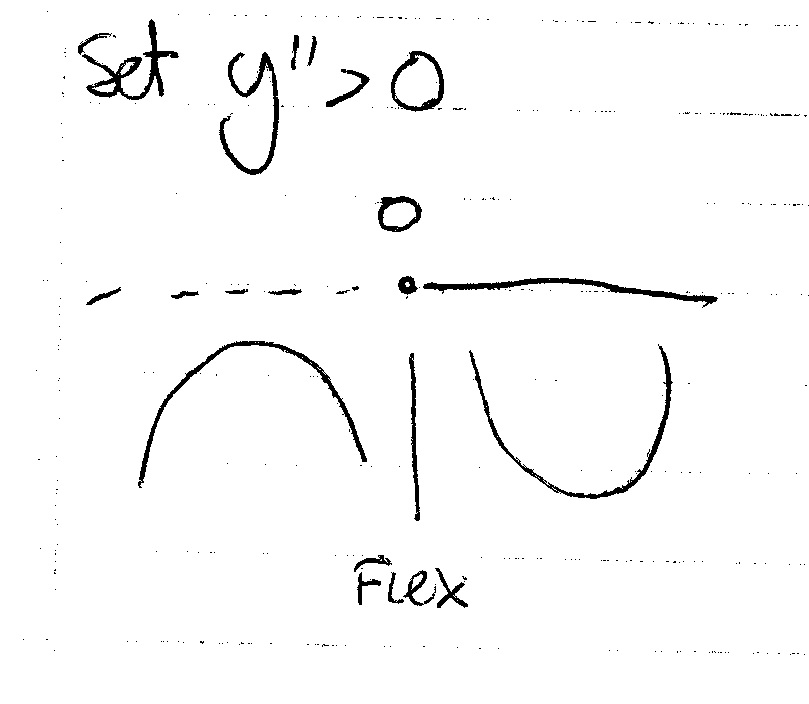
You use the second derivative to find inflection points:
Setting it equal to zero you get the point of inflection:
And finally the graph: