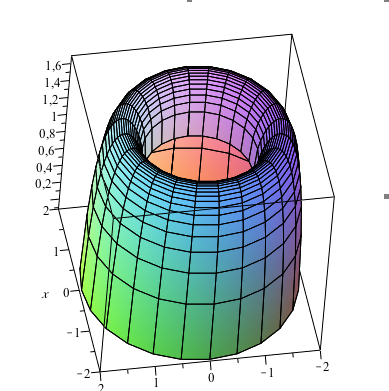
How do you graph #F(x,y)=sqrt(x^2+y^2-1)+ln(4-x^2-y^2)#?
1 Answer
Mar 26, 2015
Hello,
-
Let
#Sigma# the surface of your function#F# : it's a surface of revolution because#F(x,y) = f(r)# where#r = sqrt(x^2+y^2)# . Precisely,#f(r) = sqrt(r^2-1) + ln(4-r^2)# -
First, plot the curve of
#f : r \mapsto sqrt(r^2 -1) + ln(4-r^2)# . You get
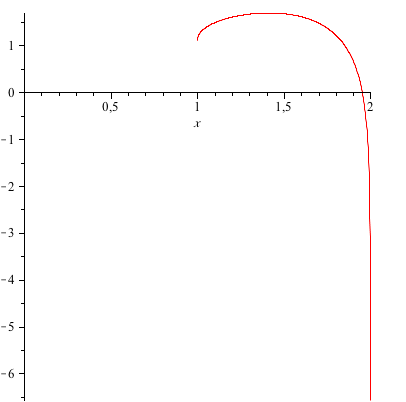
- Now, turn this curve around
#z# -axes in 3D-space. You get the surface#Sigma#