Information from #f(x)#
#f(0)=1/{1+1}=1/2 Rightarrow# y-intercept: #1/2#
#f(x) > 0 Rightarrow# x-intercept: none
#lim_{x to infty}e^x/{1+e^x}=1 Rightarrow# H.A.: #y=1#
#lim_{x to -infty}e^x/{1+e^x}=0 Rightarrow# H.A.: #x=0#
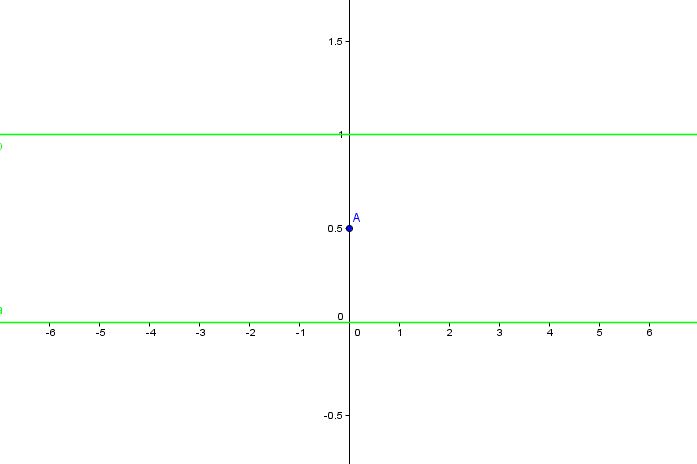
So far we have the y-intercept (in blue) and H.A.'s (in green):
Information from #f'(x)#
#f'(x)={e^xcdot(1+e^x)-e^xcdot e^x}/{(1+e^x)^2}=e^x/(1+e^x)^2>0#
#Rightarrow# #f# is always increasing.
Information from #f''(x)#
#f''(x)={e^x cdot (1+e^x)^2-e^xcdot2(1+e^x)e^x}/{(1+e^x)^4}#
#={e^x(1+e^x)(1-e^x)}/{(1+e^x)^4}={e^x(1-e^x)}/{(1+e^x)^3}#
#f''(x)>0# on #(-infty,0)# and #f''(x)<0# on #(0, infty)#
#f# is concave upward on #(-infty,0)# and downward on #(0, infty)#.
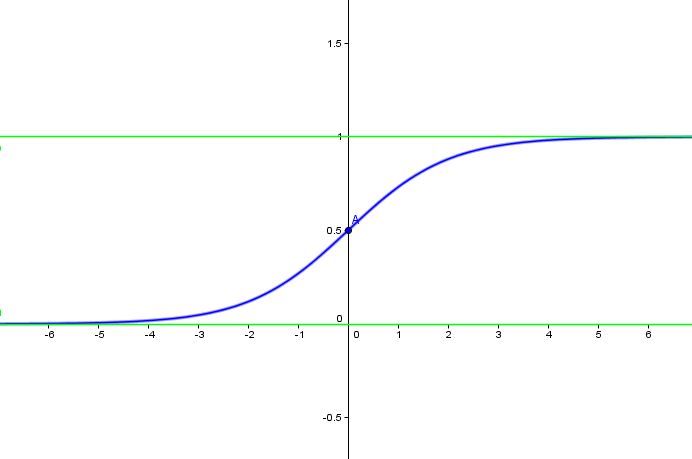
Hence, we have the graph of #f# (in blue):