Question

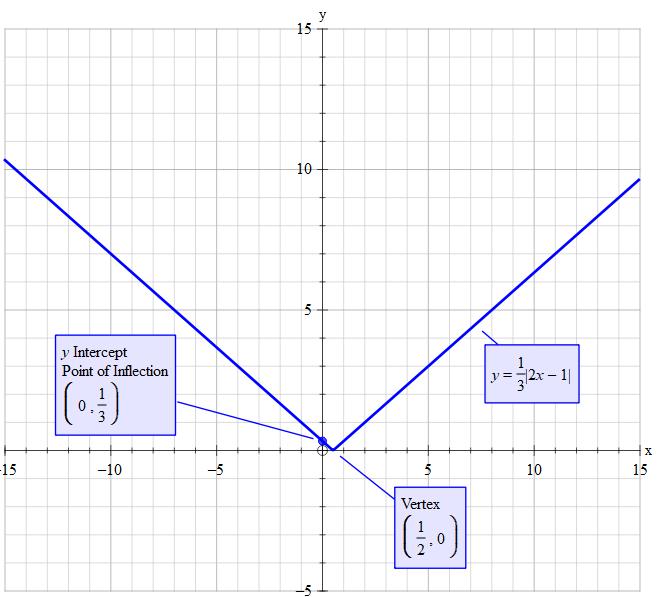
How do you graph, find the zeros, intercepts, domain and range of `f(x)=1/3abs(2x-1)`?

Answer 1

domain `{x, x in(-oo,+oo)}`
range `color(white)("d") {y, y in[0,+oo)}`

See explanation.

Explanation:

This is of graph type `vv`.

The part `|2x-1|` is always positive so `1/3|2x-1|` is also always
positive. Thus `y>=0`

`color(blue)("Determin the vertex")`

Set `y=0=1/3|2x-1|`

Multiply both sides by `3/1`

`y=0=|2x-1|`

`y=0=|0|`

So `2x-1=0=>x=1/2`

So the the vertex of `vv` is at `(x,y)->(1/2,0)`

Thus the vertex is on the x-axis. There is no plot below the x-axis.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Determine the y-intercept")`

Set `x=0` giving:

`y=1/3|0-1|`

`y=1/3xx(+1) = 1/3`

`y_("intercept")->(x,y)=(0,1/3)`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Plot two graphs but cit them off so that there is no line below the x-axis

Line 1 `y=1/3(2x-1)` where `x<=0`
Line 2 `y=1/3(2x-1)` where `x>=0`