How do you graph systems of inequalities?
1 Answer
When we say
Similarly, if we say
If there are two inequalities, each of them will mark some points on the coordinate plane. But some of the points on the coordinate plane will be marked by both of them. This means, those points are satisfying both of the inequalities so those points are our solution set.
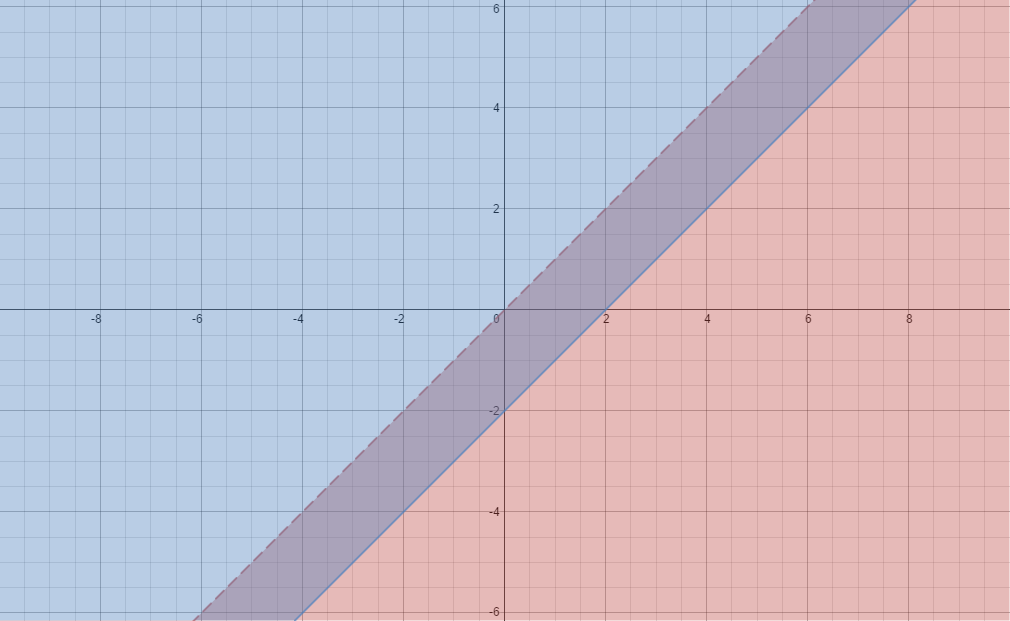
Example
To graph
We will graph
Then, the coordinate plane will be divided in two parts by the line. Now select a random point from each part.
Lets say
Lets test these points with
So the points at the part where
graph{y < x [-10, 10, -5, 5]}
Now lets continue with
We will use the base line
Then we will select
Test them:
So the points at the part where
graph{y>=x-2 [-10, 10, -5, 5]}
Now you'll see the intersection of the shaded areas. Shade it with another color and thats it.