Question

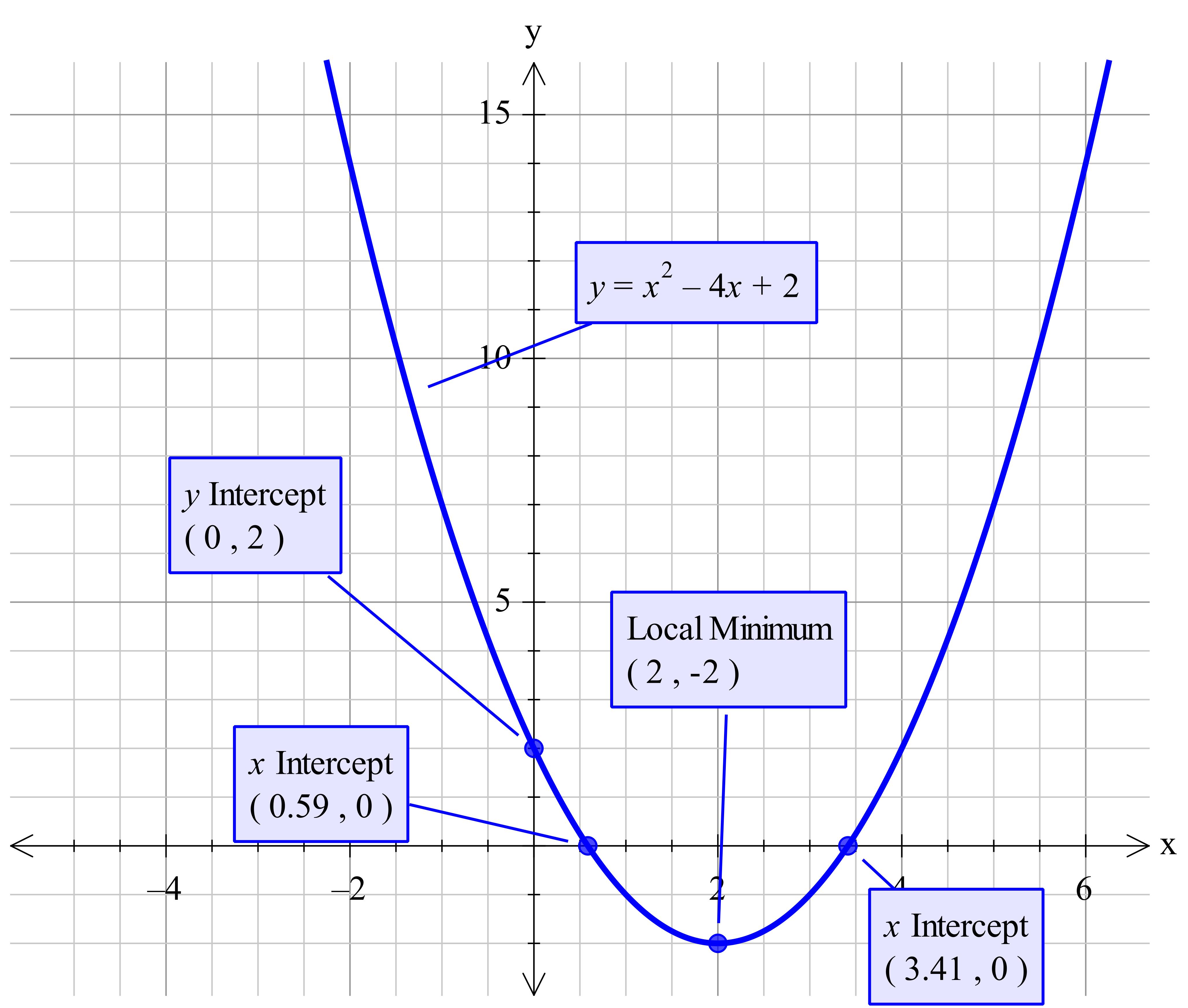
How do you graph the parabola `g(x) = x^2 - 4x + 2` using vertex, intercepts and additional points?

Answer 1

While we're in standard form, let's find the y intercept. This is found by making `x = 0`:

`y = 0^2 - 4(0) + 2 = 2`

Hence, the y intercept is at `y = 2`, or `(0, 2)`.

Now, let's convert to vertex form by completing the square.

`y = x^2 - 4x + 2`

`y = 1(x^2 - 4x + n - n) + 2`

`n = (b/2)^2`

`n = (-4/2)^2`

`n = 4`

`y = 1(x^2 - 4x + 4 - 4) + 2`

`y = 1(x ^2 - 4x + 4) - 4 + 2`

`y = 1(x^2 - 4x + 4) - 2`

`y = 1(x - 2)^2 - 2`

In vertex form, `y = a(x - p)^2 + q`, the vertex is located at `(p, q)`. Hence, the vertex will be at `(2, -2)`.

As for the x intercepts, we have to make `y = 0` and solve:

`0 = 1(x - 2)^2 - 2`

`2 = (x - 2)^2`

`+-sqrt(2) = x - 2`

`x = +-sqrt(2) + 2`

Hence, there will be x intercepts as `(2 + sqrt(2), 0)` and `(2 - sqrt(2), 0)`.

Finally, before graphing, you may find it helpful to prepare a table of values so that you can graph more accurately. It may look like the following.

Let's assume that you're working on the interval `[-1, 3]`:

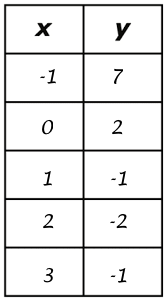
You can obviously use a larger or a smaller table of values, it just depends on what interval of the function your teacher wants you to graph.

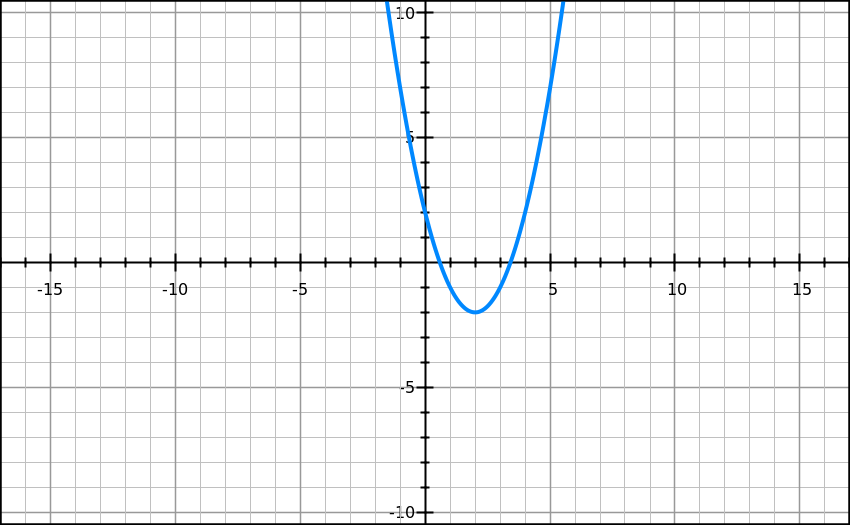
Here is the graph of the function:

Practice exercises:

`1.` Graph the following functions, identifying the vertex, intercepts, and if necessary preparing a table of values.

a) `y = -2x^2`

b) `y = 3x^2 - 2`

c) `y = -4x^2 + 5x`

d) `y = 2x^2 + 4x - 1`

e) `y = -1/4x^2 - 3x + 5`

Hopefully this helps, and good luck!

Answer 2

Demonstrating a different approach to find the vertex

`"Vertex "->(x,y)=(2,2))`
As the coefficient of `x^2` is positive then the graph of of general shape `uu`. Thus the vertex is a minimum ( the only one `->` Absolute Minimum)

`y_("intercept")=2`

`x_("intercept")=2+sqrt(2)" and "2-sqrt(2)" " larr" exact values"`

`x_("intercept")~~3.41 and x~~0.59" to 2 decimal places"`

Explanation:

As it is not specified how you determine the vertex there is an alternative approach which part way to completing the square.

Consider the general case `y=ax^2+bx+c`

Write this as `y=a(x^2+b/ax)+c`

The `x_("vertex")=(-1/2)xxb/a`

Then by substitution determine `y_("vertex")`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)(" Determine the vertex")`

Given:`" "y=x^2-4x+2`

In this case `a=1=> b/a=-4/1=-4`

`=> x_("vertex")=(-1/2)xx(-4)=+2`

`=>y_("vertex") = (4)^2-4(4)+2= 2`

`color(red)("Vertex "->(x,y)=(2,2))`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Determine "y_("intercept"))`

Reading directly off the constant for `y=x^2-4x+2`

`color(red)(y_("intercept")=2)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Determine "x_("intercepts")`
There are three options

1. Factorise - Not always easy to spot the values!
2. Use the formula
3. Completing the square.

AS the other solution uses completing the square I will use the formula method. Well worth committing to memory. I did this by making sure I wrote it out each time I practised a question. It has stayed with me for life!

general case `y=ax^2+bx+c`

where `x=(-b+-sqrt(b^2-4ac))/(2a)`

where `a=1; b=-4; c=2` giving:

`x=(-(-4)+-sqrt((-4)^2-4(1)(2)))/(2(1))`

`x=(4+-sqrt(16-8))/2" "=" "2+-(2sqrt(2))/2`

`color(red)(x=2+sqrt(2)" and "x=2-sqrt(2)" " larr" exact values")`

`color(red)(x~~3.41 and x~~0.59" to 2 decimal places")`