Generally when a point is mentioned in polar coordinates, it is in the form #(r,theta)# i.e. we move at an angle of #theta# and then at a distance of #r# from pole (equivalent to point #(0,0)# in Cartesian coordinates). #r# is then always taken as positive.
Here although the angle is mentioned as #120^@# and it means the point should be in second quadrant in Cartesian coordinates, but as #r# is mentioned as #-1#, it means moving one unit in opposite direction (i.e. in fourth quadrant) and point, say #N(-1,120^@)# should appear as follows.
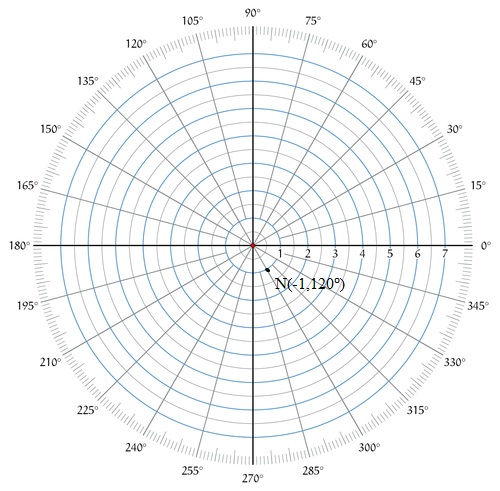
This is equivalent to #(-cos120^@,-sin120^@)# i.e. #(1/2,-sqrt3/2)# in Cartesian coordinates.

