How do you graph the system of linear inequalities #2x+1>=y# and #x<5# and #y<x+2#?
1 Answer
Draw solid or dashed lines corresponding to equations, then test the origin,
Explanation:
One way to graph a system of linear equations like this is to actually start by drawing them as if they were equalities first.
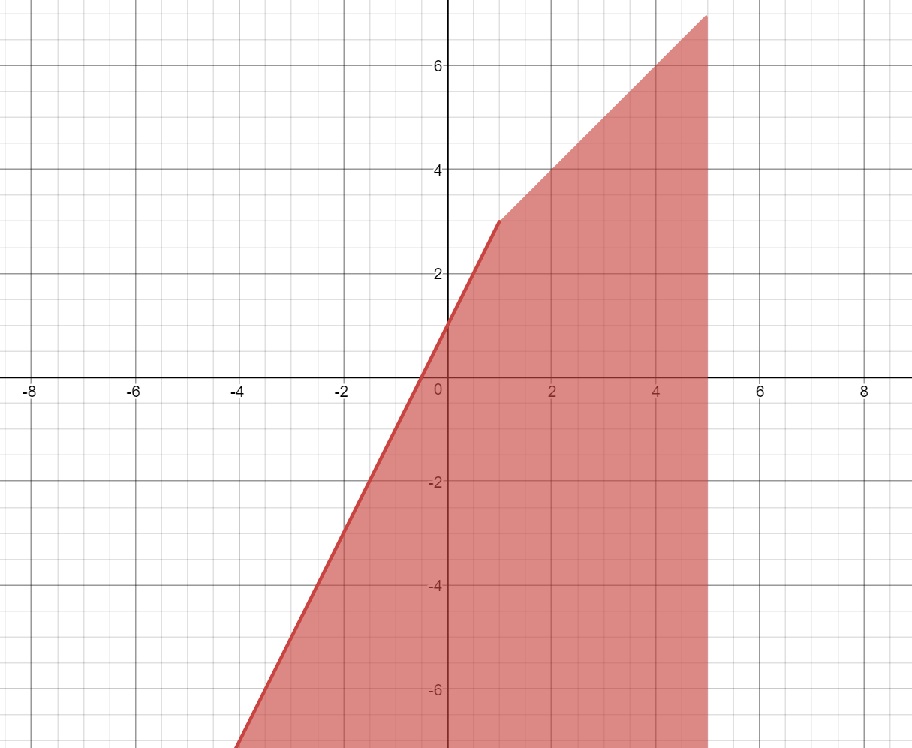
The inequality
Testing the point
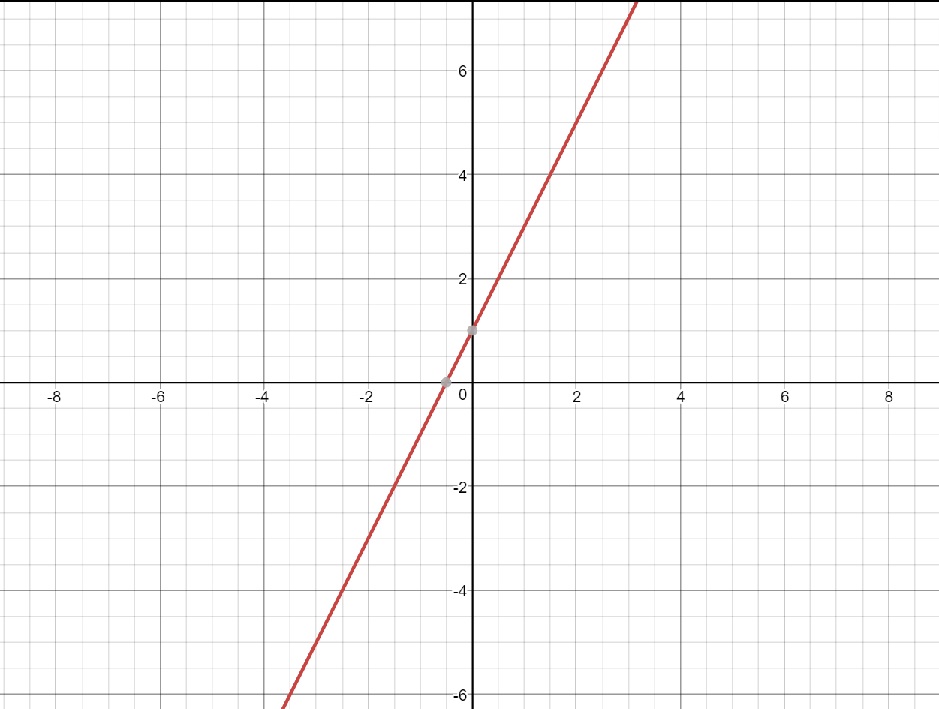
Again, assume
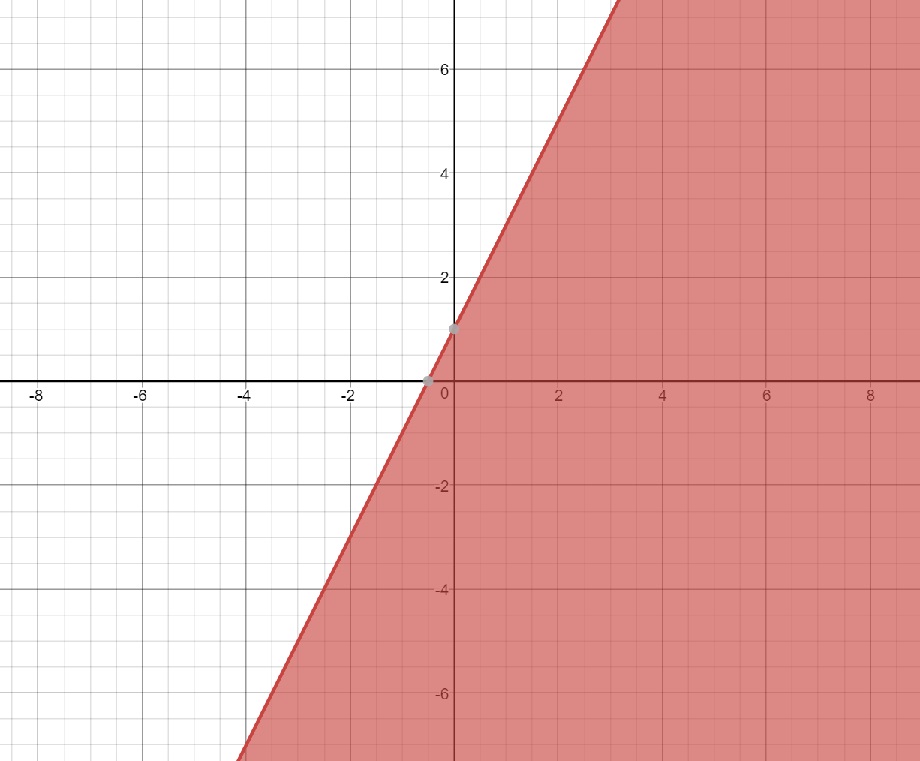
This time, the graph is dashed because you were given
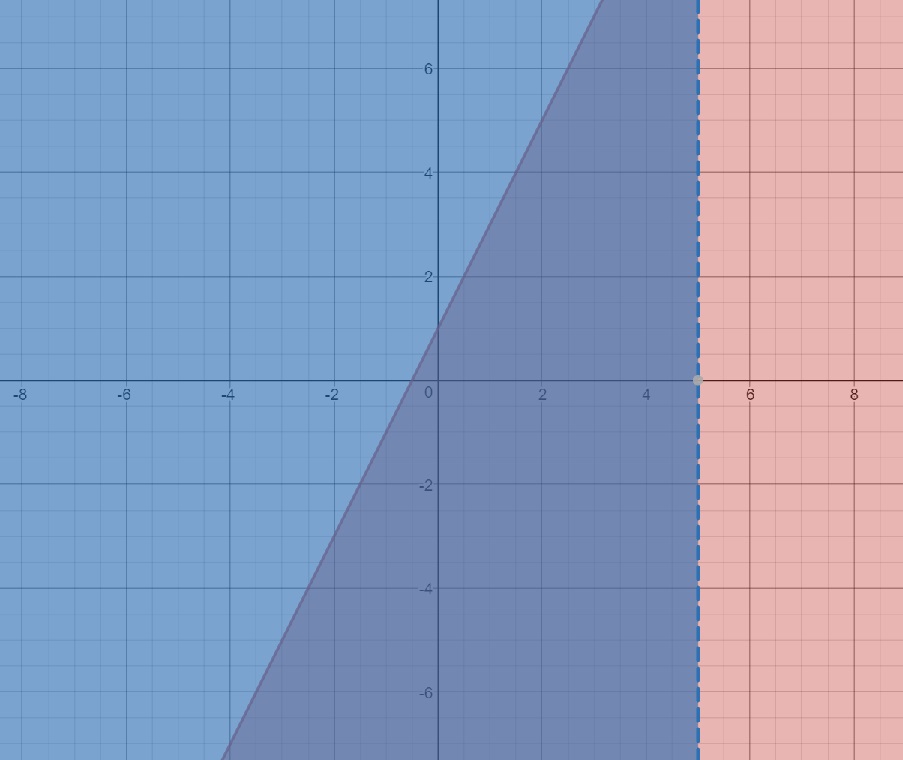
Finally, pretending to graph
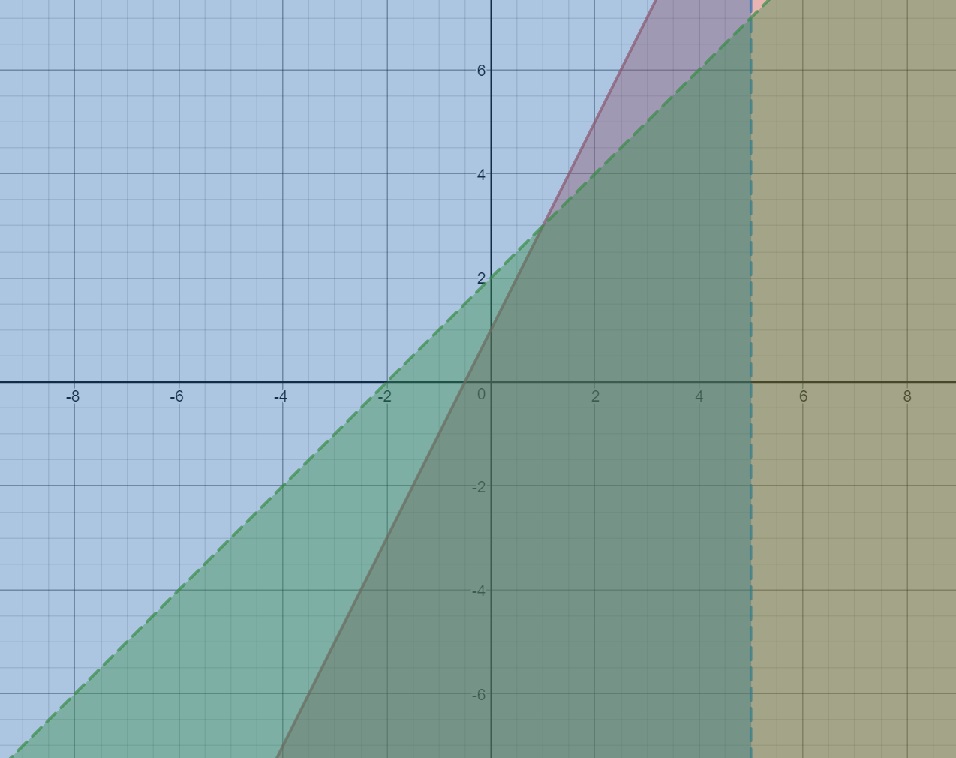
Finally, if we are to find out where ALL THREE inequality are true, you simply look for the solution where ALL THREE shaded parts overlap. That occurs here: