How do you graph to solve the equation on the interval #[-2pi,2pi]# for #tanx=1#?
1 Answer
Aug 1, 2017
(
Explanation:
Solving for x:
When the tangent of an angle is 1, we know that the lengths of the non hypotenuse sides are equal and have the same sign. So: 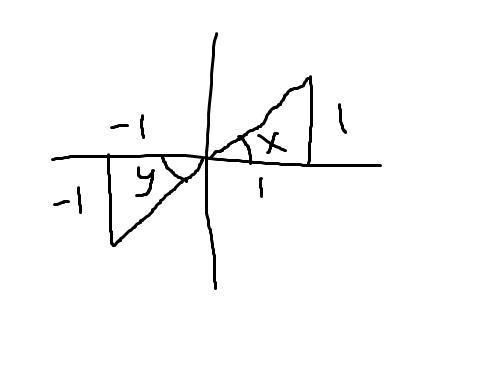 Please excuse the MS Paint
Please excuse the MS Paint
We know that the values of angles x and y are
(

