How do you graph #(x^2 / 4) - (y^2 / 9) =1#?
1 Answer
Jan 21, 2017
This hyperbola will open East-West and be centered at the origin.
Explanation:
You will move right and left 2 units from center to find the vertices. This comes from
Then, go up and down 3 units (
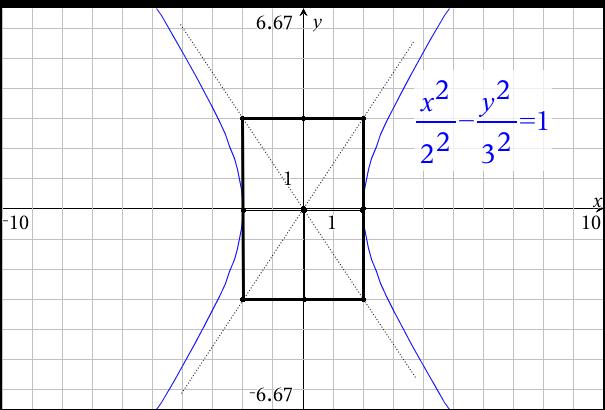
This graph was created in TI-nspire, with a template for graphing the conic sections and other relations. I didn't plot any points except for the vertices at (2,0) and (-2,0). If you are required to have more precision, make a table for ordered pairs.

