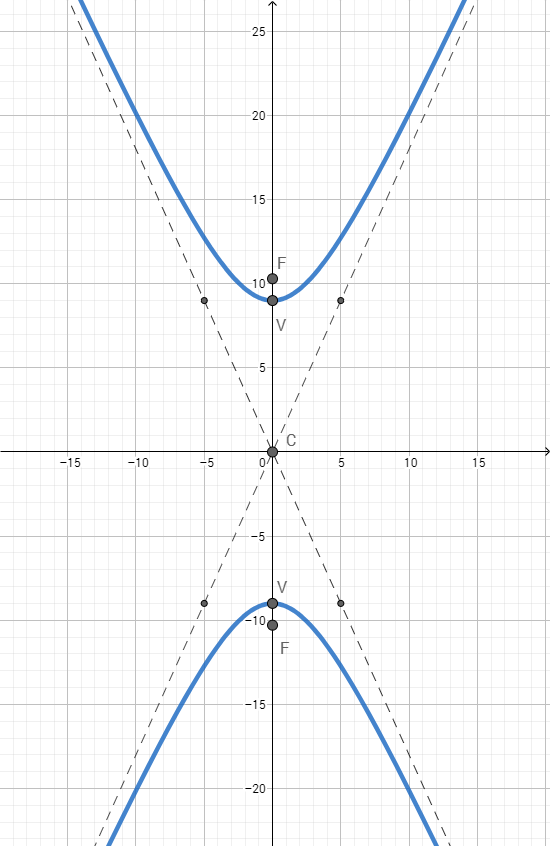
This is a hyperbola equation, which you can tell from the fact that there are both #x^2# and #y^2# terms, and that there is a minus #-# sign between them. Furthermore, because the positive term is the #y^2# term, you can tell that this hyperbola will have branches opening up and down (the traditional #y# direction).
There are a number of tricks to use to help draw the graph of any hyperbola. Most of these come from identifying some important values from the standard form of the hyperbola equation. That form is this:
#(y-y_c)^2/b^2 - (x-x_c)^2/a^2 = 1#
In this formula, the point made from #(x_c,y_c)# indicates the center of the hyperbola. The graph of the hyperbola does not go through the center, but it is an important point for other reasons we'll see shortly. Since the equation for this problem does not have any numbers in the numerators by the #x# and #y#, we know both #x_c# and #y_c# are 0. The center is at #(0,0)#.
Next, we identify the #a# and #b# values. Simply match them up, and you can see that #b# = 9 and #a# = 5. (Note how the general form has #b^2# and #a^2# in the denominators, so we solve for #b# and #a# using square roots.
Next, there's an important value called the focus distance, which is a measure of how far to travel from the center to draw the two focus points. That is denoted by the value #c#, and follows this relationship:
#c^2 = b^2 + a^2#
Note how it looks like the Pythagorean Formula (and in this case it sort of is), but be careful because ellipses have a similar formula which uses subtraction. Reminder tip: It has the opposite operation in the middle between #a# and #b# than the formula for the hyperbola itself has!
For this problem:
#c^2 = 81 + 25 = 106#
#c = +-sqrt(106) ~~+-10.3#
We have everything we need to draw a reasonable graph. Follow these steps:
1) Draw a light pencil mark at the center #(0,0)#.
2) Since this hyperbola opens up and down, move up the focus distance 10.3 from the center #(0,0)# and draw a dot/point at #(0, sqrt(106))#. This is the top focus point. Draw another dot/point a distance of 10.3 down from the center at #(0,-sqrt(106))# to represent the bottom focus point.
3) From the center, move up by #b# to #(0,9)# and draw a dot. This is the top vertex. Now, move to the right by #a# (i.e. 5), and draw a light pencil mark at #(5,9)#. Next, from the vertex point, move left this time by 5 and draw another light pencil mark at #(-5,9)#.
4) From the center, move down this time by #b# to #(0,-9)# and draw a dot. This is the bottom vertex. Like the last time, move to the right by 5 and draw a light pencil mark at #(5,-9)#, then move left by 5 from the vertex point and draw a 4th light pencil mark at #(-5,-9)#. You've just lightly marked out the 4 corners of a rectangular box that is 10 wide and 18 tall, centered at #(0,0)#
5) Using a ruler, line up the ruler so that you can draw a straight line from one corner of that rectangle to the opposite corner of the rectangle. Drawing a dashed line, draw a line across your paper along that path. Then, turn your ruler and line it up with the other two corners of the rectangle and draw another dashed line. You've now drawn the asymptotes of the hyperbola; these are two dashed lines that the graph of the hyperbola bends towards at the edges of the graph paper, but never touches.
6) Time to draw the hyperbola. Go to the top vertex at #(0, 9)# and draw a bowl shape, where the edges of the bowl open to the top of the paper, and each edge of the bowl should move close to the dashed asymptotes, but not touch it. The bowl should be contained in the top "V" shape made by the two asymptotes. The "bottom" of the bowl should sit on the top vertex point, and the top focus point should be sitting inside the bowl but not touching it. Then, draw an upside down bowl in the bottom "V" shape, with the top of the bowl sitting on the bottom vertex point, and again with the bottom focus point sitting inside of the bowl, but not touching it.
7) Erase the lightly drawn points if you are being graded on neatness and style points.