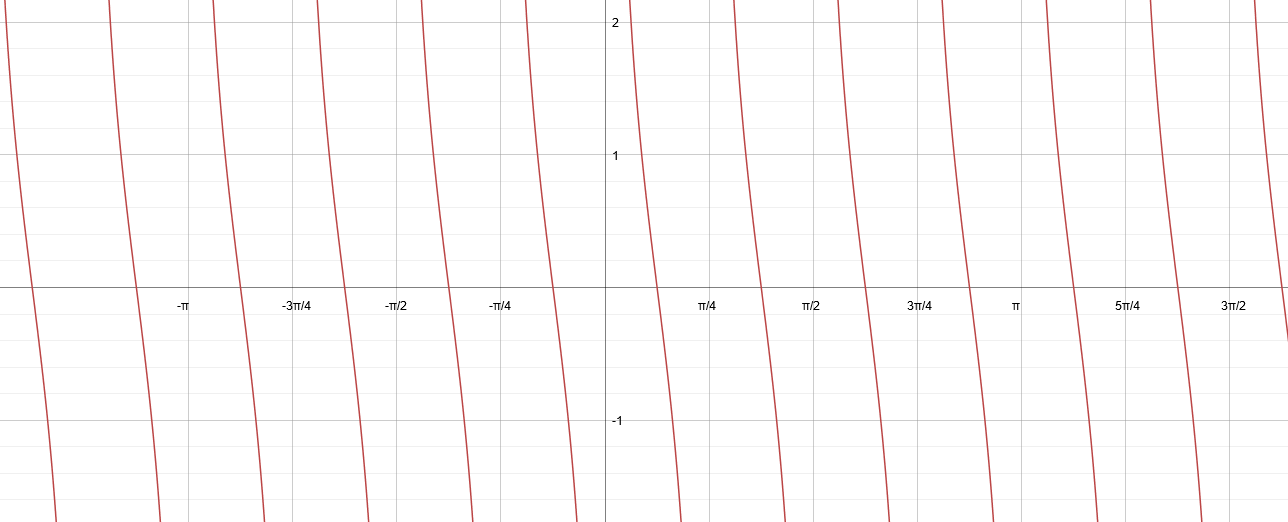
How do you graph #y=2cot4x#?
1 Answer
Oct 7, 2017
Explanation:
Using
#a *cot(bx+c)+d# ,
where:
#a=2# #b=4# #c=0# #d=0# Period
#=pi/b=pi/4# ... One cycle completes at#pi/4# Phase shift
#=c/b=0/4=0# ...Phew! that means no problemVertical shift
#=d=0# ... Again no problem!
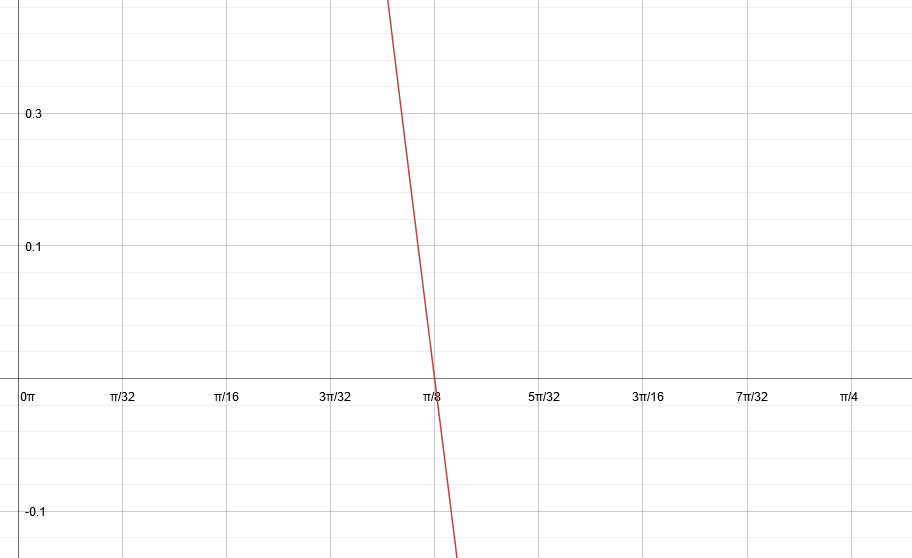
At
#pi/8# , (half of the period),#y = 0 #
At
#pi/16# , (half of the#pi/8# ),#y = a=2 # At
#(3pi)/16# , (batween#pi/8# and the period),#y = -a=-2 #
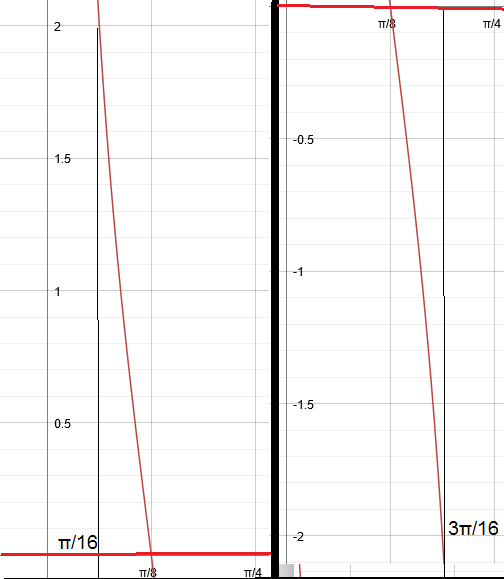
Three points are
#-> (pi/16,2), (pi/8,0), ((3pi)/16,-2)#
Therefore,