Question

How do you graph `y=4csc2x`?

Answer 1

Please see the explanation.

Explanation:

Given:

`color(red)(y = f(x) = 4 csc(2x)`

How to draw a graph for this trigonometric function?

Note that `color(green)(y = f(x) = csc(x)` is the base function.

Observe that `color(blue)(csc(x) = 1/sin(x)`

Analyze the graph below:

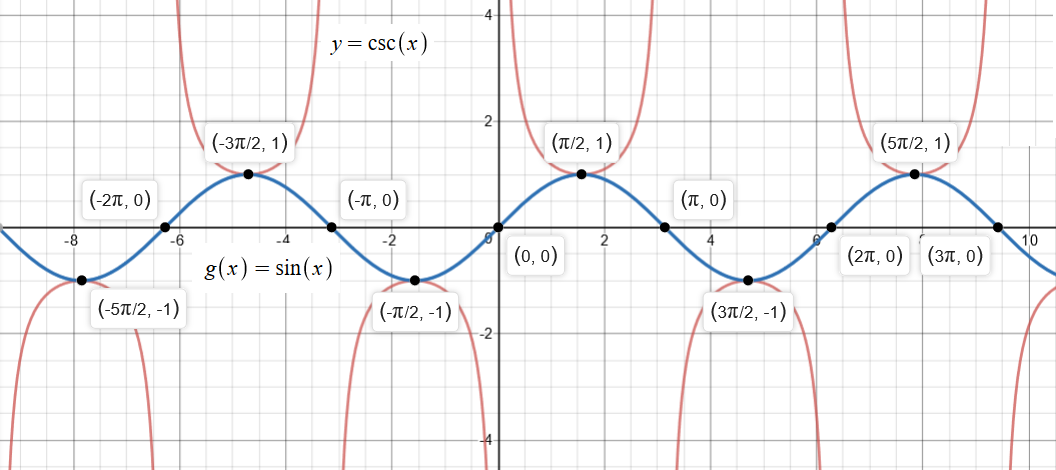
Note that the function `y=f(x)=sin(x)` has `zeros` at `x=kpi`, where `k` is an integer.

The function `y=f(x)=csc(x)` has `color(blue)"No "` `color(blue)(zeros`.

For both the functions `sin(x) and csc(x)`, Period `= 2pi`.

Graph of the function `csc(x)` does not have a maximum or a minimum value, there is `color(blue)"No "` `color(blue)(amplitude`.

If values of `sin(x)` is available, one can figure out point by point what the values of `csc(x)` are.

The function goes to infinity periodically and is symmetric with the origin.

At values of `x` for which `sin(x) = 0`, the function `csc(x)` is undefined.

The x-intercept of `y=sin(x)` and the asymptotes of `y=csc(x)` are the same.

Next, consider the given trigonometric function:

`color(blue)(y = f(x) = 4 csc(2x)`

Use the form:

A Csc(BX - C) + D.

The variables used gives us the Amplitude and Period.

`A=4; B=2; C=0 and D=0` (using the given trigonometric function).

Amplitude = None

Period `= (2pi)/B=(2pi)/|2| = pi`

Vertical Shift = D = 0

Frequency `=1/(Period) = 1/pi`

To draw the graph, we can select a few points as shown below:

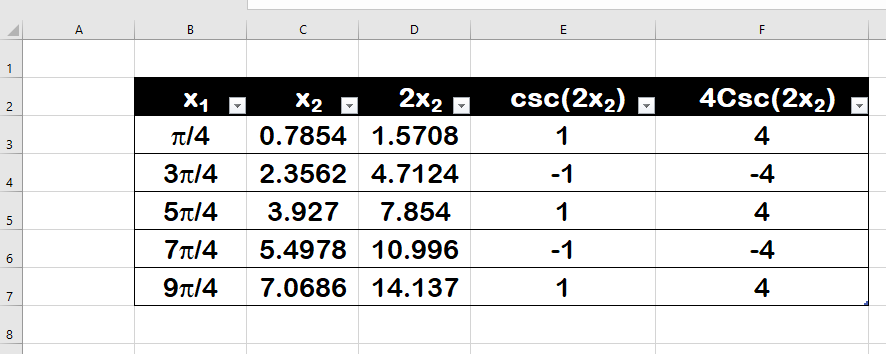
`csc(x)` has only Vertical Asymptotes.

Vertical Asymptote = `x=(pi n)/2`, where n is an integer.

Graph of `color(blue)(y = f(x) = 4 csc(2x)`

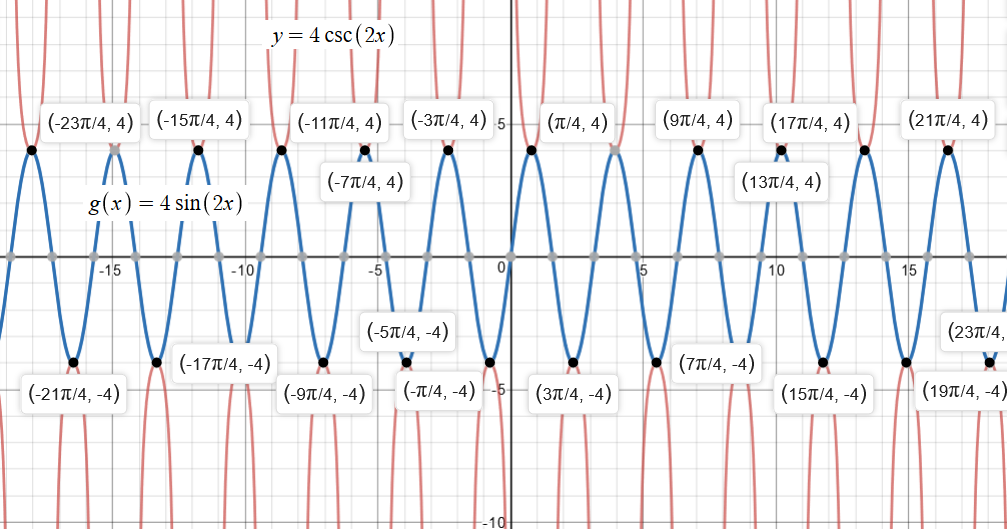
x-intercepts and y-intercepts = None