Question

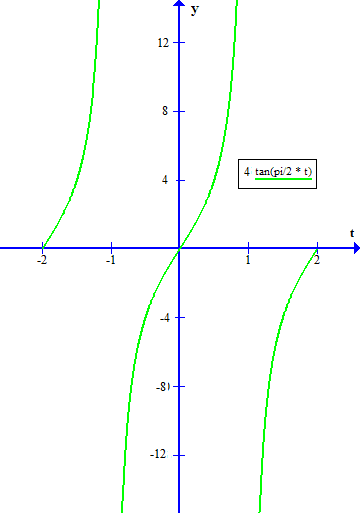
How do you graph `y=4tan(pi/2t)` over the interval `[-2,2]`?

Answer 1

(see below)

Explanation:

If we let `theta=pi/2t`
then `tin[-2,2]`
is equivalent to `thetain[-pi,+pi]`
and we know `y=tan(theta), thetain[-pi,+pi]` looks like:

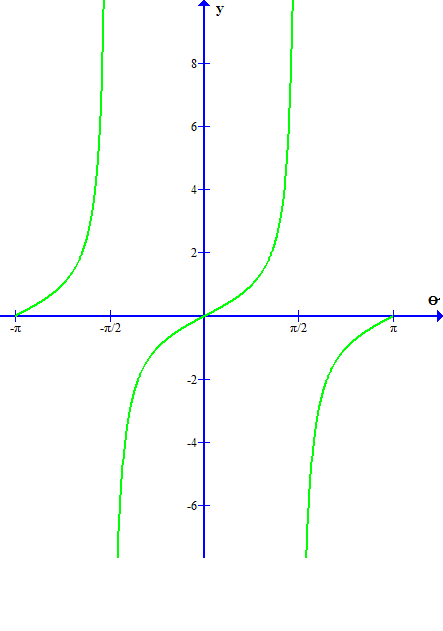
Replacing the horizontal axis with the `t` variable based scale:

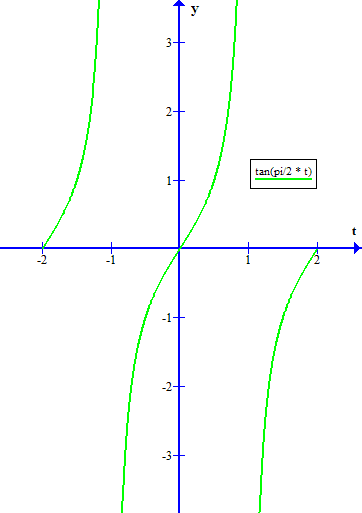
Replacing `y=tan(pi/2t)` with `y=4tan(pi/2t)`
simply pushes every `y` coordinate value `4` further away from the horizontal axis;
the easiest way to show this is to modify the scale along the vertical axis to `4` times their previous values: