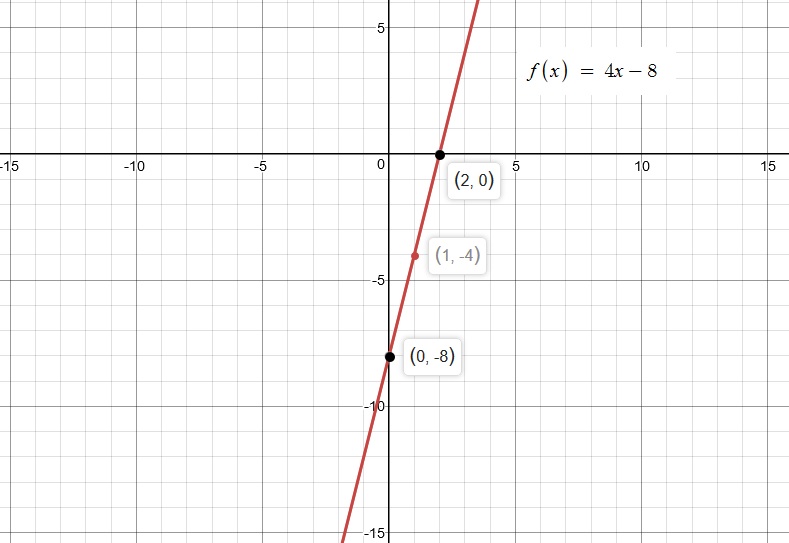
How do you graph #y=4x-8#?
1 Answer
Refer to the graph with Slope(m) = 4 and Y-Intercept
Explanation:
Also,
We need to graph
We observe that it is already in Slope-Intercept Form.
Hence, Slope =
Y-Intercept
Go to the graph and plot the point the point
Then rise 4 and run 1. Plot the point
Then again "rise 4" and then "run" 1. Plot the point
Join all these points on the graph and you will find a straight line. graph{4x - 8 [-19.75, 20.25, -14.88, 5.12]}
Also refer to an additional graph available with my suggested solution with points plotted.
Hope this helps.