Question

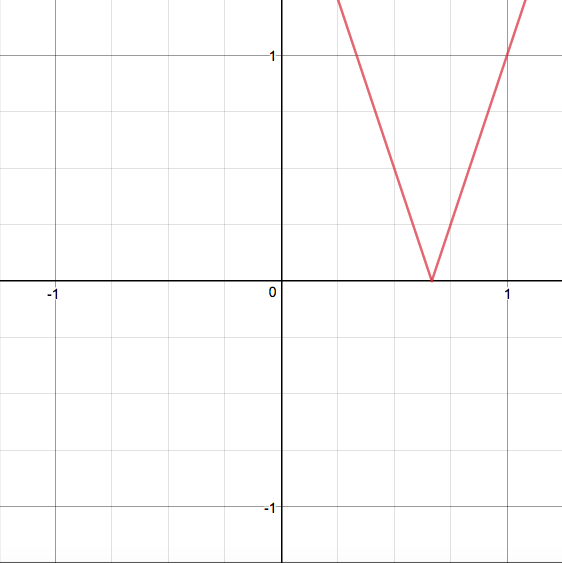
How do you graph `y=abs(3x-2)`?

Answer 1

Seperate the function into a piecewise function containing two separate functions with different domains, then graph each function with their domains.

Explanation:

Firstly, let's have a look at what the absolute value means in this case, as what is called a "piecewise function":

`y = |3x - 2| {(3x - 2, 3x - 2 ≥ 0), (-(3x - 2), 3x - 2 < 0) :}`

We could expand the negative sign over on `-(3x - 2)`:

`y = |3x - 2| {(3x - 2, 3x - 2 ≥ 0), (-3x + 2, 3x - 2 < 0) :}`

Having a look at the inequalities on the right side, we could simplify them. Let's start with the first one:

`3x - 2 ≥ 0`

Add both sides by `2`:

`3x - 2 + 2 ≥ 0 + 2`

`3x ≥ 2`

Then divide by `3`:

`(3x)/3 ≥ 2/3`

`x ≥ 2/3`

And put that back:

`y = |3x - 2| {(3x - 2, x ≥ 2/3), (-3x + 2, 3x - 2 < 0) :}`

We could be sure that the other one is solved similarly, except with a different symbol:

`y = |3x - 2| {(3x - 2, x ≥ 2/3), (-3x + 2, x < 2/3) :}`

Since both are linear equations, we'd only need two points to plot each. Let's start by plotting the "extreme" point:

if `x = 2/3`, then `y = 3(2/3) - 2 = 2 - 2 = 0`

So we have `(2/3, 0)`:

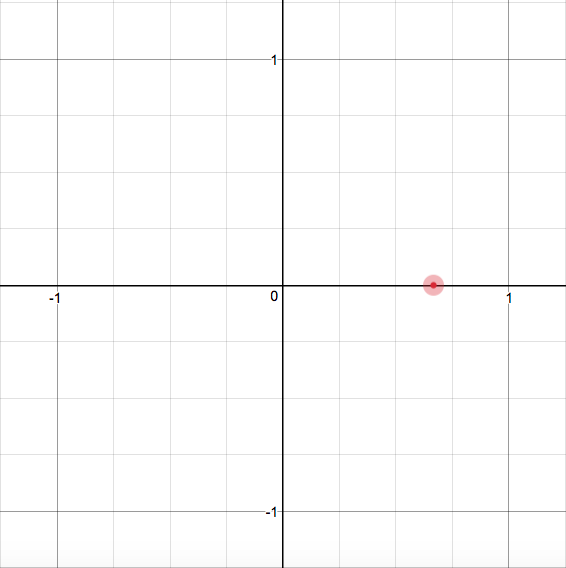
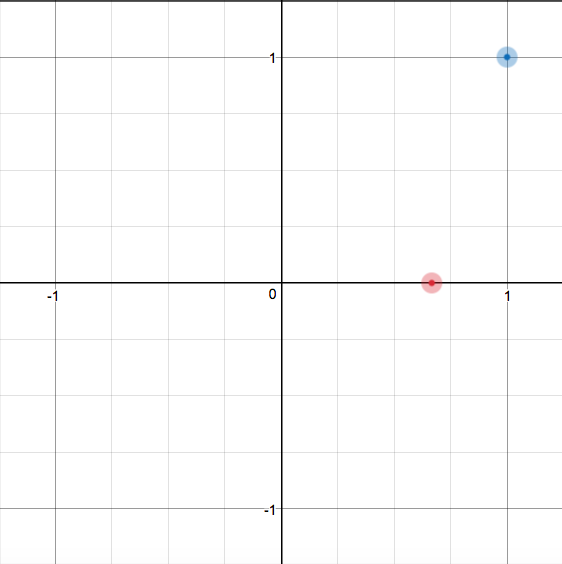
Looking at our piecewise function, we could see that the first equation should be graphed only on the right of this point, and the second equation only on the left of this point. Since this point we have plotted is part of the first equation, we just need anoter point.

Let's pick `x = 1 = 3/3`:

`y = 3x - 2 rarr 3(1) - 2 = 3(3/3) - 2 = 3 - 2 = 1`

So we have `(1, 1)`:

And we can connect these two points to form the first equation's line:

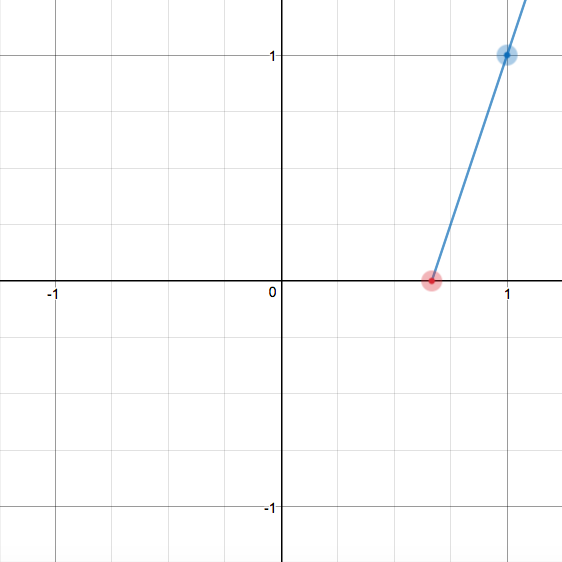
Notice, we have cut off the line by the time it reaches `x = 2/3`, because in our piecewise function, this first equation is only for `x ≥ 2/3`.

Looking at the second equation, we need a number less than `2/3`... how about `1/3`?

`y = -3x + 2 rarr y = -3(1/3) + 2 = -1 + 2 = 1`

So we have `(1/3, 1)`:

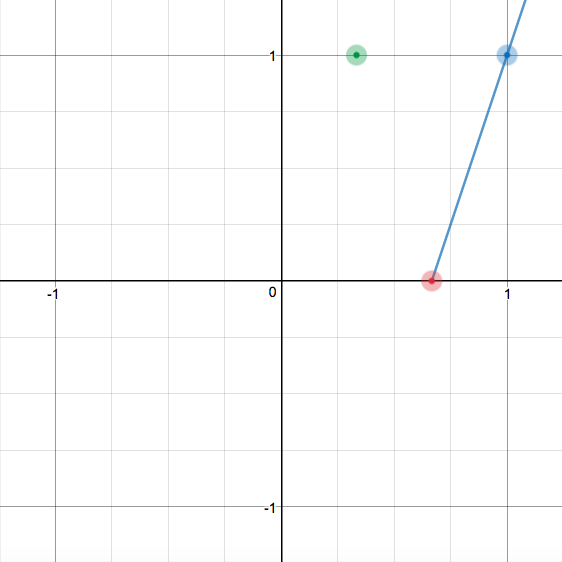
Hmm, we need another point... `x = 1/2`?

`y = -3x + 2 rarr y = -3(1/2) + 2 = -3/2 + 4/2 = 1/2`

Interesting! We have `(1/2, 1/2)`:

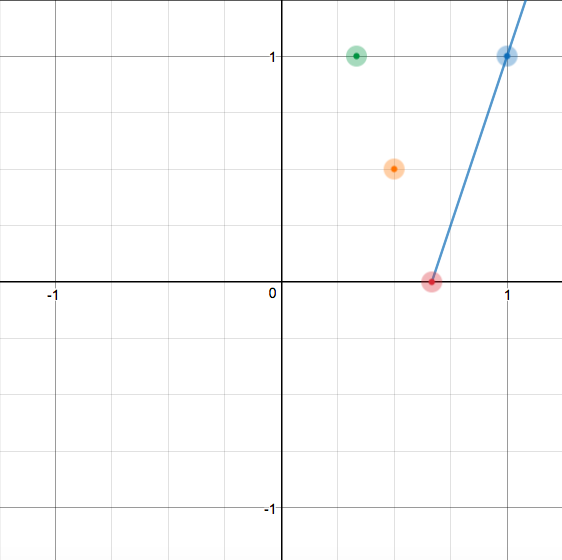
And we can connect the points to graph the second equation, also cutting it off at `x = 2/3`:

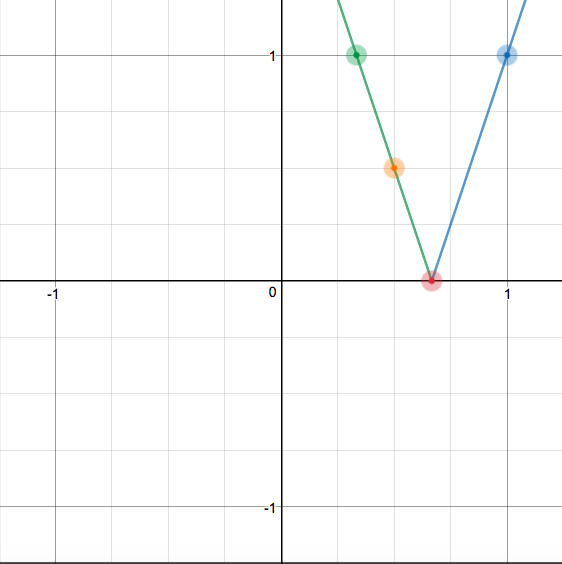
Ah, they both actually shared `(2/3, 0)`, so you could use that fact next time you graph these kinds of equations. Making things neater, here's what our final graph looks like: